|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЕРОНЕЗЕ ОТОБРАЖЕНИЕЗначение ВЕРОНЕЗЕ ОТОБРАЖЕНИЕ в математической энциклопедии: специальное регулярное отображение проективного пространства; названо в честь Дж. Веронезе (G. Veronese). Пусть n, т - целые положительные числа, задаваемый формулами где
в Этот факт позволяет использовать В. о. для сведения нек-рых задач о гиперповерхностях к случаю гиперплоских сечений. Лит.:[1] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972. И. В. Долгачев. |
|
|
|

 а
а  - проективные пространства над произвольным полем (или над кольцом целых чисел), рассматриваемые как схемы,
- проективные пространства над произвольным полем (или над кольцом целых чисел), рассматриваемые как схемы,  - проективные координаты в
- проективные координаты в  - проективные координаты в
- проективные координаты в  . Отображение Веронезе есть морфизм
. Отображение Веронезе есть морфизм 

 В инвариантных терминах В. о. может быть определено как регулярное отображение, задаваемое полной линейной системой
В инвариантных терминах В. о. может быть определено как регулярное отображение, задаваемое полной линейной системой  , где
, где  - гиперплоское сечение в
- гиперплоское сечение в  . В. о. является замкнутым вложением, его образ
. В. о. является замкнутым вложением, его образ  наз. многообразием Веронезе и задается уравнениями
наз. многообразием Веронезе и задается уравнениями 
 Напр.,
Напр.,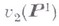 есть кривая с уравнением
есть кривая с уравнением  Степень многообразия Веронезе равна
Степень многообразия Веронезе равна  . Для любой гиперповерхности
. Для любой гиперповерхности
 ее образ относительно В. о.
ее образ относительно В. о.  является сечением многообразия Веронезе
является сечением многообразия Веронезе 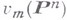 гиперплоскостью
гиперплоскостью 