|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЕКТОРНОЕ ПОЛЕЗначение ВЕКТОРНОЕ ПОЛЕ в математической энциклопедии: на многообразии M- сечение касательного расслоения Пример 1. Для карты
Пример 2. Для карты где определяется формулой он удовлетворяет соотношениям: в частности Каждое В. п. Xиндуцирует на Млокальный поток- семейство диффеоморфизмов окрестности U такое, что - интегральный путь В. п. X, т. е. где
Каждое В. п. определяет дифференцирование Ли LX тензорного поля типа и скобка Ли В. п. без особенностей порождает на Минтегрируемую одномерную дифференциальную систему и ассоциированную с ней Пфаффа систему. Обобщением понятия В. п. на многообразии является В. п. вдоль отображения Лит.:[1] Годбийон К., Дифференциальная геометрия и аналитическая механика, пер. с франц., М., 1973; [2] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [3] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967; [4] Номидзу К., Группы Ли и дифференциальная геометрия, пер. с англ., М., I960; [5] Постников М. М., Введение в теорию Морса, М., 1971; [6] Хелгасон С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964. А. Ф. Щекутьев. |
|
|
|

 . Множество В. п. образует модуль над кольцом Fдифференцируемых функций на М.
. Множество В. п. образует модуль над кольцом Fдифференцируемых функций на М. многообразия Мопределяется i-е базисное В. п. д/дxi по формуле
многообразия Мопределяется i-е базисное В. п. д/дxi по формуле 
 есть i-й базисный касательный вектор к Мв точке р, и любое В. п. однозначно представляется в виде
есть i-й базисный касательный вектор к Мв точке р, и любое В. п. однозначно представляется в виде 
 наз. компонентами В. п. Xв карте
наз. компонентами В. п. Xв карте  . В. п. является дифференцированием кольца F, вследствие чего множество В. п. образует относительно операции коммутирования (скобки Ли) алгебру Ли.
. В. п. является дифференцированием кольца F, вследствие чего множество В. п. образует относительно операции коммутирования (скобки Ли) алгебру Ли. и
и  функция
функция  определяется формулой
определяется формулой 
 - частная производная по
- частная производная по 
 наз. производной от
наз. производной от  по направлению X. Пример 3. Для карты
по направлению X. Пример 3. Для карты  и
и  коммутатор (скобка Ли) [X, Y]В. п.
коммутатор (скобка Ли) [X, Y]В. п.




 для
для  и
и 

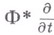 - - В. п., касательное к отображению
- - В. п., касательное к отображению  . И наоборот, В. п. Xассоциировано с локальным потоком
. И наоборот, В. п. Xассоциировано с локальным потоком  - вариацией отображения
- вариацией отображения  ; при этом
; при этом
 со значениями в векторном пространстве (инфинитезимальное преобразование
со значениями в векторном пространстве (инфинитезимальное преобразование 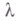 ), соответствующее локальному потоку
), соответствующее локальному потоку  частными случаями к-рого являются действие В. п. на
частными случаями к-рого являются действие В. п. на 


 - сечение расслоения
- сечение расслоения  , индуцированного
, индуцированного 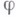 , а также тензорное поле типа
, а также тензорное поле типа  - сечение ассоциированного с
- сечение ассоциированного с  при помощи функтора
при помощи функтора  расслоения
расслоения  .
.