|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЕЙЛЯ ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИЗначение ВЕЙЛЯ ПОЧТИ ПЕРИОДИЧЕСКИЕ ФУНКЦИИ в математической энциклопедии: класс Если а есть В. п. п. ф. Существуют (см. [3]) В. п. п. ф., не представимые в виде (*). Лит.:[1] Wеу1 Н., "Math. Ann.", 1926, Bd 97, S. 338-56; [2] Левитан Б. М., Почти периодические функции, М., 1953; [3] Левитан Б. М., Степанов В. В., "Докл. АН СССР", 1939, т. 22, № 5, с. 229-32. Е. А. Бредихина. |
|
|
|

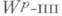 комплекснозначных почти периодических функций
комплекснозначных почти периодических функций 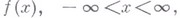 суммируемых со степенью р в каждом конечном интервале действительной оси и обладающих, при нек-ром
суммируемых со степенью р в каждом конечном интервале действительной оси и обладающих, при нек-ром 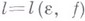 , относительно плотным множеством
, относительно плотным множеством 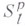 ,
, 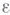 -почти периодов;определены Г. Вейлем [1]. Класс Wp- ппявляется расширением класса Степанова почти периодических функций. В. п. п. ф. связаны с метрикой
-почти периодов;определены Г. Вейлем [1]. Класс Wp- ппявляется расширением класса Степанова почти периодических функций. В. п. п. ф. связаны с метрикой 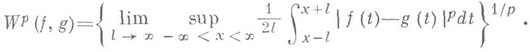
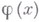 нулевая функция в метрике
нулевая функция в метрике 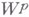 , т. е.
, т. е.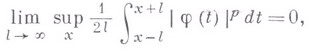
 - почти периодическая функция Степанова, то
- почти периодическая функция Степанова, то 