|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЕЙЛЯ ОБЛАСТЬЗначение ВЕЙЛЯ ОБЛАСТЬ в математической энциклопедии: - частный случай аналитического полиэдра. Ограниченная область Dп-мерного комплексного пространства имеют размерность 2п-1; 3) ребра В. <о. D, т. е. пересечения любых k( Лит.:[1] Well A., "Math. Ann.", 1935, Bd 111, S. 178- 82; [2] Шабат Б. В., Введение в комплексный анализ, ч. 1-2, 2 изд., М., 1976; [3] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964. М. Ширинбеков, |
|
|
|

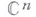 наз. областью Вейля, если существует
наз. областью Вейля, если существует  таких функций
таких функций 
 голоморфных в фиксированной окрестности
голоморфных в фиксированной окрестности  замыкания
замыкания  , что:
, что:
 ) различных граней, имеют размерность
) различных граней, имеют размерность  Совокупность всех n-мерных ребер В. о. наз. остовом В. о. Для В. о. справедливо интегральное Бергмана - Вейля представление. Названа по имени А. Вейля, к-рому принадлежат первые важные результаты для этой области [1].
Совокупность всех n-мерных ребер В. о. наз. остовом В. о. Для В. о. справедливо интегральное Бергмана - Вейля представление. Названа по имени А. Вейля, к-рому принадлежат первые важные результаты для этой области [1].