"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АДАМАРА МАТРИЦА
Значение АДАМАРА МАТРИЦА в математической энциклопедии:
- квадратная матрица 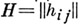 порядка ге, элементы
порядка ге, элементы 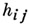 к-рой суть +1 или - 1, и такая, что имеет место равенство
к-рой суть +1 или - 1, и такая, что имеет место равенство

где Н Т - транспонированная матрица Н, а In - единичная матрица порядка п. Равенство 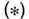 эквивалентно утверждению, что любые две строки Нортогональны. А. м. названы по имени
эквивалентно утверждению, что любые две строки Нортогональны. А. м. названы по имени 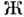 . Адамара, доказавшего [1], что определитель
. Адамара, доказавшего [1], что определитель 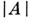 матрицы
матрицы 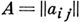 порядка и, элементы
порядка и, элементы 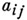 к-рой суть комплексные числа, удовлетворяет не равенству Адамара:
к-рой суть комплексные числа, удовлетворяет не равенству Адамара:
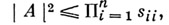
где
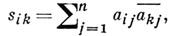
akj - элемент, сопряженный 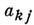 (см. А дамара теорема об определителях). В частности, если
(см. А дамара теорема об определителях). В частности, если 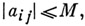 то
то 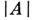
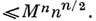 Отсюда следует, что А. м. есть квадратная матрица из
Отсюда следует, что А. м. есть квадратная матрица из 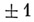 порядка пс максимальным абсолютным значением определителя, равным
порядка пс максимальным абсолютным значением определителя, равным 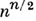 . Свойства А. м.: 1) из
. Свойства А. м.: 1) из 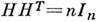 следует
следует 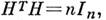 и наоборот; 2) перестановка строк или столбцов и умножение элементов к.-л. строки или столбца А. м. на - 1 сохраняют свойство матрицы быть А. м.; 3) прямое произведение двух А. м. есть снова А. м., порядок к-рой равен произведению порядков сомножителей. Иными словами, если
и наоборот; 2) перестановка строк или столбцов и умножение элементов к.-л. строки или столбца А. м. на - 1 сохраняют свойство матрицы быть А. м.; 3) прямое произведение двух А. м. есть снова А. м., порядок к-рой равен произведению порядков сомножителей. Иными словами, если 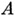
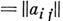 и
и 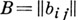 суть А. м. порядков ти п соответственно, то
суть А. м. порядков ти п соответственно, то 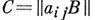 есть А. м. порядка тп. А. м., у к-рой первая строка и первый столбец состоят из +1, наз. нормализованной. Порядок А. м. n=1, 2 или
есть А. м. порядка тп. А. м., у к-рой первая строка и первый столбец состоят из +1, наз. нормализованной. Порядок А. м. n=1, 2 или 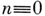 (mod 4). Нормализованные А. м. порядков 1 и 2 суть:
(mod 4). Нормализованные А. м. порядков 1 и 2 суть:
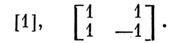
Существование А. м. доказано для нескольких классов значений п(см., напр., [2], [3]). Предположение о существовании А. м. для любого 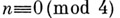 остается (70-е гг. 20 в.) недоказанным. Методы построения А. м. рассмотрены в [2]. А. м. используются при построении нек-рых типов блок-схем[2] и кодов [3]. Так, А. м. порядка
остается (70-е гг. 20 в.) недоказанным. Методы построения А. м. рассмотрены в [2]. А. м. используются при построении нек-рых типов блок-схем[2] и кодов [3]. Так, А. м. порядка 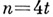 эквивалентна адамаровой (
эквивалентна адамаровой (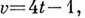
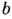
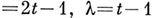 )-конфигурации.
)-конфигурации.
Обобщенной А. м. наз. квадратная матрица 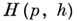 порядка h, элементами к-рой являются корни р- ойстепени из единицы и к-рая удовлетворяет равенству
порядка h, элементами к-рой являются корни р- ойстепени из единицы и к-рая удовлетворяет равенству 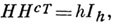 где
где 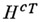 - транспонированная матрица Нс сопряженными элементами, а
- транспонированная матрица Нс сопряженными элементами, а 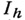 - единичная матрица порядка h. Для обобщенных А. м. справедливы свойства, аналогичные 1) и 3) (см. [4]).
- единичная матрица порядка h. Для обобщенных А. м. справедливы свойства, аналогичные 1) и 3) (см. [4]).

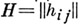 порядка ге, элементы
порядка ге, элементы 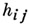 к-рой суть +1 или - 1, и такая, что имеет место равенство
к-рой суть +1 или - 1, и такая, что имеет место равенство 
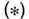 эквивалентно утверждению, что любые две строки Нортогональны. А. м. названы по имени
эквивалентно утверждению, что любые две строки Нортогональны. А. м. названы по имени 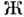 . Адамара, доказавшего [1], что определитель
. Адамара, доказавшего [1], что определитель 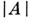 матрицы
матрицы 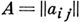 порядка и, элементы
порядка и, элементы 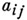 к-рой суть комплексные числа, удовлетворяет не равенству Адамара:
к-рой суть комплексные числа, удовлетворяет не равенству Адамара: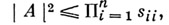
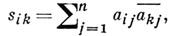
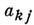 (см. А дамара теорема об определителях). В частности, если
(см. А дамара теорема об определителях). В частности, если 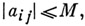 то
то 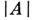
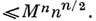 Отсюда следует, что А. м. есть квадратная матрица из
Отсюда следует, что А. м. есть квадратная матрица из 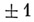 порядка пс максимальным абсолютным значением определителя, равным
порядка пс максимальным абсолютным значением определителя, равным 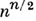 . Свойства А. м.: 1) из
. Свойства А. м.: 1) из 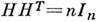 следует
следует 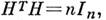 и наоборот; 2) перестановка строк или столбцов и умножение элементов к.-л. строки или столбца А. м. на - 1 сохраняют свойство матрицы быть А. м.; 3) прямое произведение двух А. м. есть снова А. м., порядок к-рой равен произведению порядков сомножителей. Иными словами, если
и наоборот; 2) перестановка строк или столбцов и умножение элементов к.-л. строки или столбца А. м. на - 1 сохраняют свойство матрицы быть А. м.; 3) прямое произведение двух А. м. есть снова А. м., порядок к-рой равен произведению порядков сомножителей. Иными словами, если 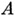
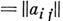 и
и 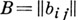 суть А. м. порядков ти п соответственно, то
суть А. м. порядков ти п соответственно, то 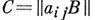 есть А. м. порядка тп. А. м., у к-рой первая строка и первый столбец состоят из +1, наз. нормализованной. Порядок А. м. n=1, 2 или
есть А. м. порядка тп. А. м., у к-рой первая строка и первый столбец состоят из +1, наз. нормализованной. Порядок А. м. n=1, 2 или 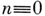 (mod 4). Нормализованные А. м. порядков 1 и 2 суть:
(mod 4). Нормализованные А. м. порядков 1 и 2 суть: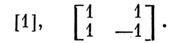
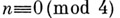 остается (70-е гг. 20 в.) недоказанным. Методы построения А. м. рассмотрены в [2]. А. м. используются при построении нек-рых типов блок-схем[2] и кодов [3]. Так, А. м. порядка
остается (70-е гг. 20 в.) недоказанным. Методы построения А. м. рассмотрены в [2]. А. м. используются при построении нек-рых типов блок-схем[2] и кодов [3]. Так, А. м. порядка 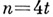 эквивалентна адамаровой (
эквивалентна адамаровой (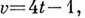
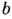
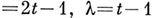 )-конфигурации.
)-конфигурации.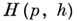 порядка h, элементами к-рой являются корни р- ойстепени из единицы и к-рая удовлетворяет равенству
порядка h, элементами к-рой являются корни р- ойстепени из единицы и к-рая удовлетворяет равенству 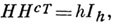 где
где 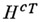 - транспонированная матрица Нс сопряженными элементами, а
- транспонированная матрица Нс сопряженными элементами, а 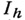 - единичная матрица порядка h. Для обобщенных А. м. справедливы свойства, аналогичные 1) и 3) (см. [4]).
- единичная матрица порядка h. Для обобщенных А. м. справедливы свойства, аналогичные 1) и 3) (см. [4]).