"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЯКОБИ ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ
Значение ЯКОБИ ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ в математической энциклопедии:
- эллиптические функции, возникшие при непосредственном обращении эллиптических интегралов в нормальной форме Лежандра. Эта задача обращения была решена в 1827 независимо К. Якоби (С. Jacobi) и, в несколько иной форме, Н. Абелем (N. Abel). Конструкция Якоби основывается на применении тета-функций.
Пусть 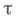 - комплексное число с
- комплексное число с 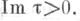 Тета-функции Якоби
Тета-функции Якоби 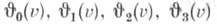 представляют собой следующие ряды, абсолютно и равномерно сходящиеся на компактах плоскости комплексного переменного v:
представляют собой следующие ряды, абсолютно и равномерно сходящиеся на компактах плоскости комплексного переменного v:
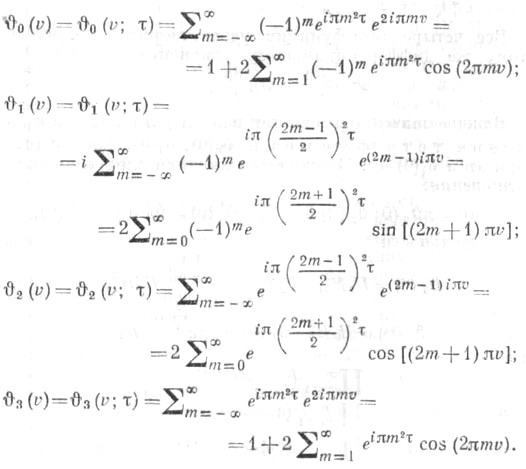
Эти ряды достаточно быстро сходятся. Обозначения 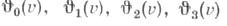 восходят к К. Вейерштрассу (К. Weierstrass). Вместо
восходят к К. Вейерштрассу (К. Weierstrass). Вместо 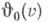 часто пишут
часто пишут 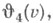 имеются и другие системы обозначений. Сам К. Якоби применял обозначения:
имеются и другие системы обозначений. Сам К. Якоби применял обозначения:
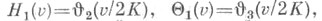 где
где 
Все тета-функции Якоби представляют собой целые трансцендентные функции комплексного переменного v, причем 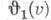 - нечетная функция, а остальные функции
- нечетная функция, а остальные функции 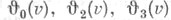 четные.
четные.
Имеют место следующие соотношения периодичности:
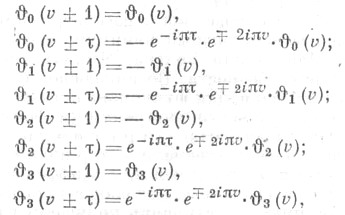
из к-рых вытекает, что тета-функции являются эллиптич. функциями III рода по Эрмиту.
Различные тета-функции связаны между собой формулами преобразования:
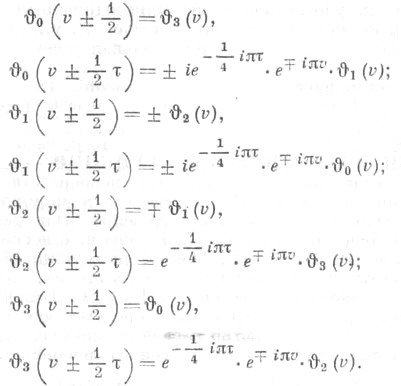
Все четыре тета-функции удовлетворяют одному и тому же дифференциальному уравнению
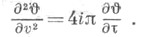
Важное значение имеют так наз. нулевые значения тета-функций 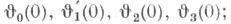 при этом
при этом 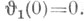 Между ними имеются следующие соотношения:
Между ними имеются следующие соотношения:
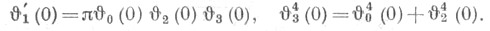
По отдельности
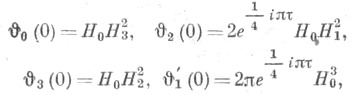
где

Функция  имеет простые нули в точках
имеет простые нули в точках 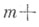
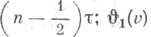 - в точках
- в точках 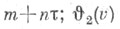 - в точкax
- в точкax 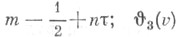 - в точках
- в точках 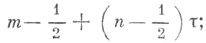
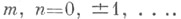
Из соотношений периодичности видно, что нек-рые отношения тета-функции будут эллиптич. функциями в собственном смысле. Основные эллиптические функции Якоби - snu(синус амплитуды). сn.(косинус амплитуды )и dnu (дельта амплитуды). Эти обозначения введены X. Гудерманом (Ch. Gudermann, 1838). Названия происходят от старых обозначений, введенных самим К. Якоби (znи==sin аmu, cnu=cos amu, dnu= amu)и позднее вышедших из употребления.
amu)и позднее вышедших из употребления.
Новое переменное исвязано с . соотношением u=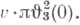 Если
Если 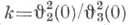 - модуль эллиптических функций, то Я. э. ф. следующим образом выражаются через тета-функции или посредством сходящихся в окрестности начала степенных рядов:
- модуль эллиптических функций, то Я. э. ф. следующим образом выражаются через тета-функции или посредством сходящихся в окрестности начала степенных рядов:
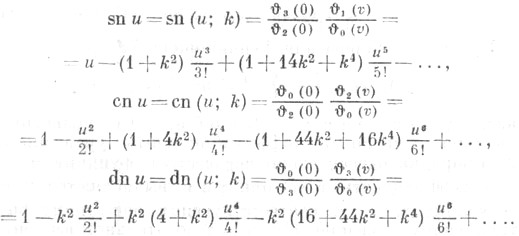
Удобные обозначения для обратных величин и отношений были введены Дж. Глейшером(J. Glaisher, 1882):
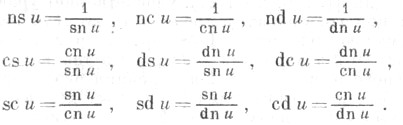
Я. э. ф. snu, сnи, dnu являются эллиптич. функциями 2-го порядка с периодами: 4K и 2iK' для snu; 4K и 2(K+iK' )для сnи; 2Ки 4iK' для dnu. Здесь K=
 - значения полных эллиптич. интегралов I рода,
- значения полных эллиптич. интегралов I рода, 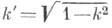 - дополнительный модуль эллиптических функций. Я. э. ф. имеют только простые полюсы, расположенные в точках 2mK+(2n+1)iK'; т,
- дополнительный модуль эллиптических функций. Я. э. ф. имеют только простые полюсы, расположенные в точках 2mK+(2n+1)iK'; т,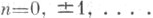
Три Я. э. ф. связаны соотношениями:
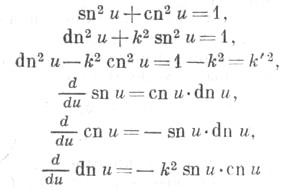
и дифференциальными уравнениями
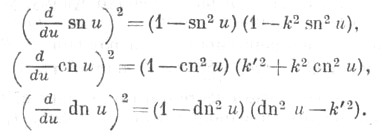
Теоремы сложения дяя Я. э. ф. имеют вид:
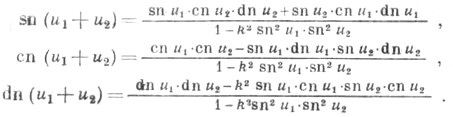
Связь Я. э. ф. с эллиптич. интегралами выражается в том, что если

- эллиптич. интеграл I рода в нормальной форме Лежандра, то его обращение имеет вид z=snu; в этом и состоял исходный пункт теории Якоби. Переменная 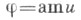 есть бесконечнозначная функция от ии наз. амплитудой эллиптического интеграла u,
есть бесконечнозначная функция от ии наз. амплитудой эллиптического интеграла u,
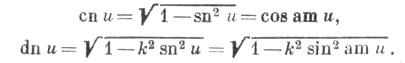
Основные соотношения между постоянными:
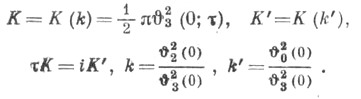
В прикладных задачах обычно задан модуль k, причем чаще всего имеет место так наз. нормальный случай 0<k<1, или задан дополнительный модуль 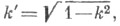 0<k'<1. Требуется найти К, К',
0<k'<1. Требуется найти К, К', 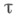 или
или 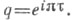 Полагая
Полагая 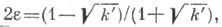 при 0<k<l имеем
при 0<k<l имеем  Для определения qполучается быстро сходящийся при
Для определения qполучается быстро сходящийся при 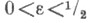 ряд
ряд
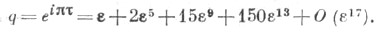
Значения полных эллиптич. интегралов . и К' определяются по формулам
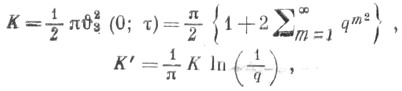
или при помощи таблиц.
При k =0 и k =1 Я. э. ф. вырождаются соответственно в тригонометрич. и гиперболич. функции:
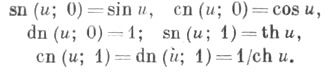
В теоретич. отношении более простое построение теории эллиптич. функций дано К. Вейерштрассом к 1802-63 (см. Вейерштрасса эллиптические функции ). При заданном модуле k, 0<k <1, инварианты Вейерштрасса e 1, е 2, е 3 вычисляются, напр., по формулам е 1= (2-k 2)/3, е 2=(2k 2-1)/3, е 3=-(1+k 2)/3, и далее g 2= -4(e 1e 2+e 2e 3+e 3e 1), g 3=4e 1e 2e 3. Полупериоды теперь определяются по формулам 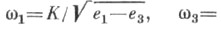
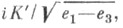 что и дает возможность вычислить все остальные величины, относящиеся к эллиптич. функциям Вейерштрасса.
что и дает возможность вычислить все остальные величины, относящиеся к эллиптич. функциям Вейерштрасса.
Лит.:[1] Jасоbi С., Fundamenta nova theoriae functionum ellipticarum, Konigsberg, 1829; Gesammelte Werke, Bd 1, В., 1881; [2] Axиезер Н. И., Элементы теории эллиптических функций, 2 изд., М., 1970; [3] Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; [4] Уиттекер Э. Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ 2 изд., ч. 2, М., 1963; [5] Еnnереr A., Elliptische Funktionen. Theorie und Geschichte, 2 Aufl., Halle/Saale, 1890; [6] Tannery J., Molk J., Elements de la theorie des functions elliptigues, t. 1-4, P., 1983-1902; [7] Журавский А. М., (Справочник по эллиптическим функциям, М.- Л., 1941; [8] Янке Е., Эмде Ф., Лёш Ф,, Специальные функции Формулы, графики, таблицы, пер. с нем., 3 изд., М., 1977.
Е. Д. Соломенцев.

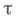 - комплексное число с
- комплексное число с 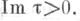 Тета-функции Якоби
Тета-функции Якоби 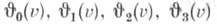 представляют собой следующие ряды, абсолютно и равномерно сходящиеся на компактах плоскости комплексного переменного v:
представляют собой следующие ряды, абсолютно и равномерно сходящиеся на компактах плоскости комплексного переменного v: 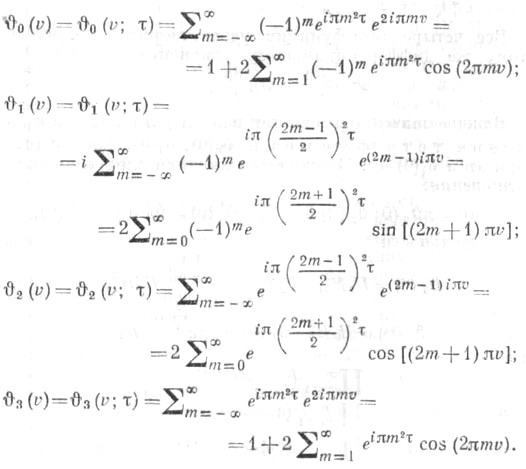
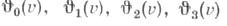 восходят к К. Вейерштрассу (К. Weierstrass). Вместо
восходят к К. Вейерштрассу (К. Weierstrass). Вместо 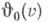 часто пишут
часто пишут 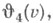 имеются и другие системы обозначений. Сам К. Якоби применял обозначения:
имеются и другие системы обозначений. Сам К. Якоби применял обозначения:
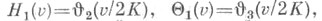 где
где 
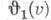 - нечетная функция, а остальные функции
- нечетная функция, а остальные функции 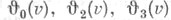 четные.
четные. 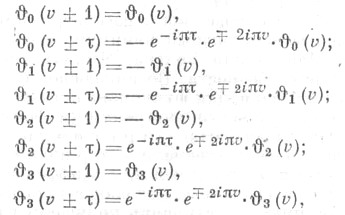
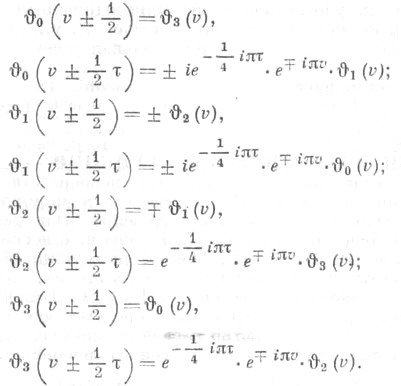
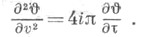
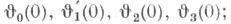 при этом
при этом 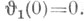 Между ними имеются следующие соотношения:
Между ними имеются следующие соотношения: 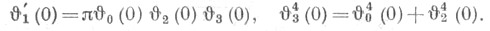
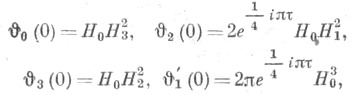

 имеет простые нули в точках
имеет простые нули в точках 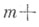
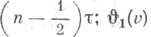 - в точках
- в точках 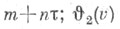 - в точкax
- в точкax 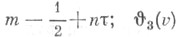 - в точках
- в точках 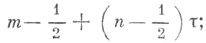
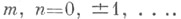
 amu)и позднее вышедших из употребления.
amu)и позднее вышедших из употребления. 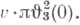 Если
Если 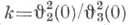 - модуль эллиптических функций, то Я. э. ф. следующим образом выражаются через тета-функции или посредством сходящихся в окрестности начала степенных рядов:
- модуль эллиптических функций, то Я. э. ф. следующим образом выражаются через тета-функции или посредством сходящихся в окрестности начала степенных рядов: 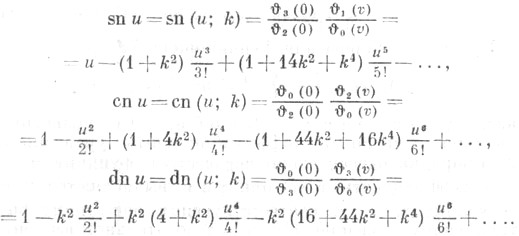
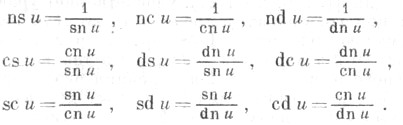

 - значения полных эллиптич. интегралов I рода,
- значения полных эллиптич. интегралов I рода, 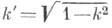 - дополнительный модуль эллиптических функций. Я. э. ф. имеют только простые полюсы, расположенные в точках 2mK+(2n+1)iK'; т,
- дополнительный модуль эллиптических функций. Я. э. ф. имеют только простые полюсы, расположенные в точках 2mK+(2n+1)iK'; т,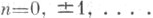
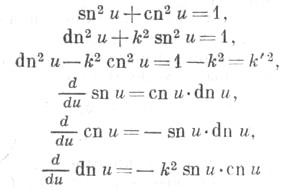
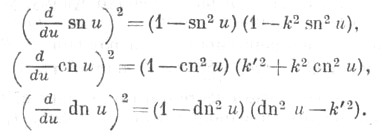
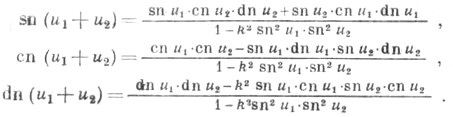

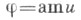 есть бесконечнозначная функция от ии наз. амплитудой эллиптического интеграла u,
есть бесконечнозначная функция от ии наз. амплитудой эллиптического интеграла u, 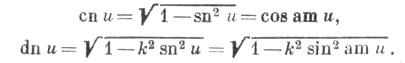
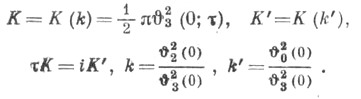
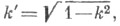 0<k'<1. Требуется найти К, К',
0<k'<1. Требуется найти К, К', 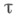 или
или 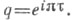 Полагая
Полагая 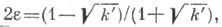 при 0<k<l имеем
при 0<k<l имеем  Для определения qполучается быстро сходящийся при
Для определения qполучается быстро сходящийся при 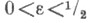 ряд
ряд 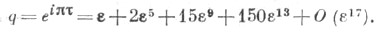
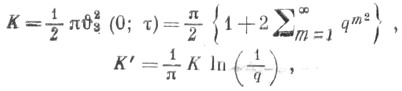
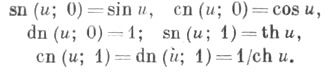
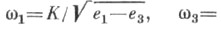
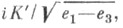 что и дает возможность вычислить все остальные величины, относящиеся к эллиптич. функциям Вейерштрасса.
что и дает возможность вычислить все остальные величины, относящиеся к эллиптич. функциям Вейерштрасса.