|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВЕБЕРА УРАВНЕНИЕЗначение ВЕБЕРА УРАВНЕНИЕ в математической энциклопедии: линейное обыкновенное дифференциальное уравнение 2-го порядка точка Решения уравнения (*) наз. функциями параболического цилиндра, или функциями Вебера - Эрмита. В частности, если v - целое неотрицательное число, то уравнению (*) удовлетворяет функция где Лит.:[1] Weber Н., "Math. Ann.", 1869, Bd 1, S. 1-36; [2] Уиттекер Э. Т., Ватсон Д ж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; [3] Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., 2 изд., М., 1974; [4] Янке Е., Эмде Ф., Леш Ф., Специальные функции. Формулы, графики, таблицы, пер. с нем., 2 изд., М., 1968. Н. X. Розов. |
|
|
|
является для него сильно особой точкой. Уравнение этого вида впервые было рассмотрено Г. Ве-бером в теории потенциала в связи с параболич. цилиндром (см. [1]); оно возникает при разделении переменных в уравнении Лапласа в параболич. координатах. В. у. заменой 
приводится к Уиттекера уравнению и представляет собой частный случай вырожденного гипергеометрического уравнения. Замена 
приводит В. у. к виду 
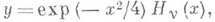
- Эрмита многочлен (см. [2] - [4]).