"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЯКОБИ УСЛОВИЕ
Значение ЯКОБИ УСЛОВИЕ в математической энциклопедии:
- необходимое условие оптимальности в задачах вариационного исчисления. Я. у. является необходимым условием неотрицательности 2-й вариации минимизируемого функционала в точке его минимума (равенство нулю 1-й вариации функционала
обеспечивается выполнением необходимых условий первого порядка - дифференциального Эйлера уравнения, трансверсальности условием, а также Вейерштрасса условием).
Пусть, напр., поставлена задача минимизации функционала
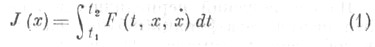
при ладанных условиях на концах

Если 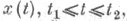 есть решение задачи (1), (2), то 1-я вариация функционала
есть решение задачи (1), (2), то 1-я вариация функционала  должна быть равна нулю, и отсюда следуют необходимые условия 1-го порядка, а 2-я вариация
должна быть равна нулю, и отсюда следуют необходимые условия 1-го порядка, а 2-я вариация
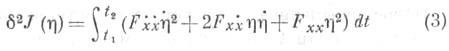
должна быть больше или равна нулю при любой кусочно гладкой функции  удовлетворяющей нулевым граничным условиям
удовлетворяющей нулевым граничным условиям
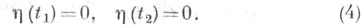
Уравнение Эйлера для функционала 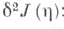
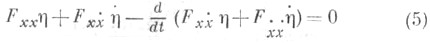
наз. уравнением Якоби. Это уравнение является линейным дифференциальным уравнением 2-го порядка относительно неизвестной функции 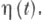
Все коэффициенты в (5) при 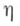 и
и  вычисляются при значениях
вычисляются при значениях  соответствующих известному оптимальному решению x(t)и, следовательно, все они являются известными функциями, зависящими от аргумента t.
соответствующих известному оптимальному решению x(t)и, следовательно, все они являются известными функциями, зависящими от аргумента t.
Функция 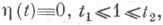 удовлетворяет уравнению Якоби при граничных условиях (4), то есть является экстремалью функционала
удовлетворяет уравнению Якоби при граничных условиях (4), то есть является экстремалью функционала  С другой стороны, для
С другой стороны, для 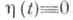 2-я вариация
2-я вариация 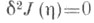 и так как для оптимального решения x(t)2-явариация неотрицательна при любых
и так как для оптимального решения x(t)2-явариация неотрицательна при любых  то функция
то функция 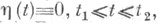 доставляет минимум функционалу
доставляет минимум функционалу 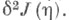 Если выполнено условие Лежандра
Если выполнено условие Лежандра 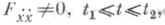 то есть x(t)является неособенной экстремалью, то при начальных условиях
то есть x(t)является неособенной экстремалью, то при начальных условиях  решение уравнения Якоби тождественно равно нулю.
решение уравнения Якоби тождественно равно нулю.
Точка t=с наз. сопряженной с точкой t=a, если существует решение уравнения Якоби, обращающееся в нуль при 2=а и t=с и не равное тождественно нулю между а и с. Согласно необходимому Я. у., если неособенная экстремаль x(t),  доставляет минимум функционалу (1), то интервал (t1, t2) не содержит точек, сопряженных с t1.
доставляет минимум функционалу (1), то интервал (t1, t2) не содержит точек, сопряженных с t1.
Практич. смысл Я. у. может быть пояснен следующим образом. Пусть Я. у. не выполняется, т. е. существует точка а, t1<а<t2, сопряженная с t1. Тогда можно было бы построить непрерывную функцию
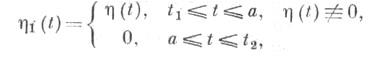
являющуюся решением уравнения (5), для к-рой  Таким образом,
Таким образом,  является ломаной экстремалью функционала
является ломаной экстремалью функционала 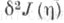 с угловой точкой при t=a. По согласно необходимому условию Вейерштрасса - Эрдмана (см. Эйлера уравнение), требующему непрерывности выражений
с угловой точкой при t=a. По согласно необходимому условию Вейерштрасса - Эрдмана (см. Эйлера уравнение), требующему непрерывности выражений  и
и  в угловой точке, при t=a должно выполняться равенство
в угловой точке, при t=a должно выполняться равенство 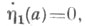 что вместе с
что вместе с 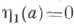 дает
дает  а это противоречит предположению .
а это противоречит предположению .
Для непосредственной проверки Я. у. следует рассматривать решение уравнения (5), удовлетворяющее начальным условиям
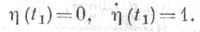
Пусть  - это решение. Для того, чтобы точка t=a,
- это решение. Для того, чтобы точка t=a, 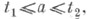 была сопряжена с t1, необходимо и достаточно, чтобы функция
была сопряжена с t1, необходимо и достаточно, чтобы функция 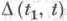 обратилась в нуль при t=a. Таким образом, выполнение Я. у. эквивалентно условию необращения в нуль решения уравнения Якоби
обратилась в нуль при t=a. Таким образом, выполнение Я. у. эквивалентно условию необращения в нуль решения уравнения Якоби  на интервале (t1, t2).
на интервале (t1, t2).
В более общем случае, когда рассматривается вариационная задача на условный минимум (задача в форме Лагранжа, Майера или Больца), формулировка Я. у. имеет нек-рые особенности. Возникающая здесь задача на минимум 2-й вариации функционала формулируется как задача на условный экстремум (в форме задачи Больца). Эта задача наз. присоединенной задачей, а ее экстремали - присоединенными экстремалями. Дифференциальные условия связи и граничные условия в присоединенной задаче на минимум 2-й вариации получаются в результате варьирования соответствующих условий исходной вариационной задачи. Определение сопряженной точки остается по форме таким же. Для неотрицательности 2-й вариации функционала на классе присоединенных экстремалей, удовлетворяющих присоединенным условиям для концов, должно выполняться Я. у., требующее, чтобы интервал (tl, t2 )не содержал точек, сопряженных с t1.
Я. у. установлено К. Якоби (С. Jacobi, 1837).
Лит.:[1] Блисс Г. А., Лекции по вариационному исчислению, пер. о англ., М., 1950; [2] Лаврентьев М. А., Люстерникc Л . А.,Курс вариационного исчисления, 2 изд., М.- Л., 1950.
И. Б. Вапнярский.

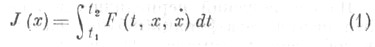

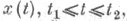 есть решение задачи (1), (2), то 1-я вариация функционала
есть решение задачи (1), (2), то 1-я вариация функционала  должна быть равна нулю, и отсюда следуют необходимые условия 1-го порядка, а 2-я вариация
должна быть равна нулю, и отсюда следуют необходимые условия 1-го порядка, а 2-я вариация 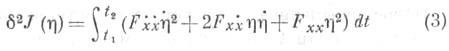
 удовлетворяющей нулевым граничным условиям
удовлетворяющей нулевым граничным условиям 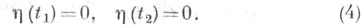
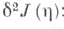
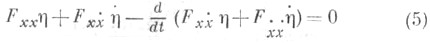
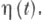
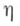 и
и  вычисляются при значениях
вычисляются при значениях  соответствующих известному оптимальному решению x(t)и, следовательно, все они являются известными функциями, зависящими от аргумента t.
соответствующих известному оптимальному решению x(t)и, следовательно, все они являются известными функциями, зависящими от аргумента t. 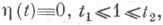 удовлетворяет уравнению Якоби при граничных условиях (4), то есть является экстремалью функционала
удовлетворяет уравнению Якоби при граничных условиях (4), то есть является экстремалью функционала  С другой стороны, для
С другой стороны, для 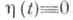 2-я вариация
2-я вариация 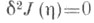 и так как для оптимального решения x(t)2-явариация неотрицательна при любых
и так как для оптимального решения x(t)2-явариация неотрицательна при любых  то функция
то функция 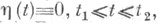 доставляет минимум функционалу
доставляет минимум функционалу 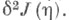 Если выполнено условие Лежандра
Если выполнено условие Лежандра 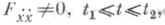 то есть x(t)является неособенной экстремалью, то при начальных условиях
то есть x(t)является неособенной экстремалью, то при начальных условиях  решение уравнения Якоби тождественно равно нулю.
решение уравнения Якоби тождественно равно нулю.  доставляет минимум функционалу (1), то интервал (t1, t2) не содержит точек, сопряженных с t1.
доставляет минимум функционалу (1), то интервал (t1, t2) не содержит точек, сопряженных с t1. 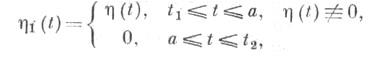
 Таким образом,
Таким образом,  является ломаной экстремалью функционала
является ломаной экстремалью функционала 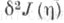 с угловой точкой при t=a. По согласно необходимому условию Вейерштрасса - Эрдмана (см. Эйлера уравнение), требующему непрерывности выражений
с угловой точкой при t=a. По согласно необходимому условию Вейерштрасса - Эрдмана (см. Эйлера уравнение), требующему непрерывности выражений  и
и  в угловой точке, при t=a должно выполняться равенство
в угловой точке, при t=a должно выполняться равенство 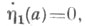 что вместе с
что вместе с 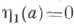 дает
дает  а это противоречит предположению .
а это противоречит предположению .
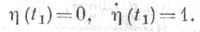
 - это решение. Для того, чтобы точка t=a,
- это решение. Для того, чтобы точка t=a, 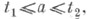 была сопряжена с t1, необходимо и достаточно, чтобы функция
была сопряжена с t1, необходимо и достаточно, чтобы функция 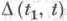 обратилась в нуль при t=a. Таким образом, выполнение Я. у. эквивалентно условию необращения в нуль решения уравнения Якоби
обратилась в нуль при t=a. Таким образом, выполнение Я. у. эквивалентно условию необращения в нуль решения уравнения Якоби  на интервале (t1, t2).
на интервале (t1, t2).