"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭРМИТА МНОГОЧЛЕНЫЗначение ЭРМИТА МНОГОЧЛЕНЫ в математической энциклопедии:
многочлены Чебышева - Эрмита,- многочлены, ортогональные на интервале  с весовой функцией k(x)=ехр(- х 2). Стандартизованные Э. м. определяются Родрига формулой с весовой функцией k(x)=ехр(- х 2). Стандартизованные Э. м. определяются Родрига формулой
 Наиболее употребительны формулы
 Первые Э. м. имеют вид
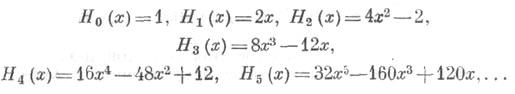 Многочлен Hn (х)удовлетворяет дифференциальному уравнению у"-2ху'+ 2ny = 0. Ортонормированные Э. м. определяются равенством

Э. м. с единичным старшим коэффициентом имеют вид 
Ряды Фурье по Э. м. внутри интервала  аналогичны тригонометрич. рядам Фурье. аналогичны тригонометрич. рядам Фурье.
В математич. статистике и теории вероятностей применяются Э. м., соответствующие весовой функции 
Определение Э. м. встречается у П. Лапласа [1]. Подробное исследование этих многочленов опубликовал П. Л. Чебышов в 1859 (см. [2]). Затем эти многочлены изучал Ш. Эрмит [3]. В. А. Стеклов [4] доказал плотность множества всех многочленов в пространстве функций, квадрат к-рых интегрируем с весом h(x)=ехр(-x2) на всей оси.
См. также Классические ортогональные многочлены.
Лит.:[1] Lарlaсе P. S., лMem. classe sci. math., phys. inst. France
|

 с весовой функцией k(x)=ехр(- х 2). Стандартизованные Э. м. определяются Родрига формулой
с весовой функцией k(x)=ехр(- х 2). Стандартизованные Э. м. определяются Родрига формулой 

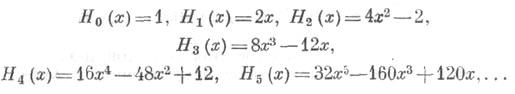


 аналогичны тригонометрич. рядам Фурье.
аналогичны тригонометрич. рядам Фурье. 