|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭПИЦИКЛОИДАЗначение ЭПИЦИКЛОИДА в математической энциклопедии: - плоская кривая, траектория точки окружности, катящейся по другой окружности и имеющей с ней внешнее касание. Параметрич. уравнения:
где r - радиус катящейся окружности, R - радиус неподвижной окружности,
В зависимости от величины модуля m=R/r получаются Э. различной формы. При т=1Э.- кардиоида, при тцелом кривая состоит из тнепересекающихся ветвей. Точки возврата А 1, А2, . . .. А т имеют полярные координаты
Если точка находится не на катящейся окружности, а лежит вне (внутри) ее, то кривая наз. удлиненной (укороченной) эпициклоидой или эпитрохоидой (см. Трохоида).Э. относится к т. н. циклоидальным кривым. Лит.:[1] Савелов А. А., Плоские кривые, М., 1960. |
|
|
|


 - угол, стягиваемый дугой между точками касания окружностей (см. рис.).
- угол, стягиваемый дугой между точками касания окружностей (см. рис.). 
 k=0,1, . . ., т-1. Вершины кривой B1, В2, . . ., В т имеют координаты
k=0,1, . . ., т-1. Вершины кривой B1, В2, . . ., В т имеют координаты 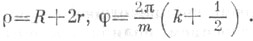 При тдробном ветви перекрещиваются; при тиррациональном число ветвей бесконечно, точка Мв исходное положение не возвращается; при трациональном Э.- замкнутая алгебраич. кривая. Длина дуги от точки A1:
При тдробном ветви перекрещиваются; при тиррациональном число ветвей бесконечно, точка Мв исходное положение не возвращается; при трациональном Э.- замкнутая алгебраич. кривая. Длина дуги от точки A1: 


