"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭНТРОПИЯ
Значение ЭНТРОПИЯ в математической энциклопедии:
- теоретико-информационная мера степени неопределенности случайной величины. Если 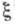 - дискретная случайная величина, определенная на нек-ром вероятностном пространстве
- дискретная случайная величина, определенная на нек-ром вероятностном пространстве  и принимающая значения x1, x2, . . . с распределением вероятностей
и принимающая значения x1, x2, . . . с распределением вероятностей 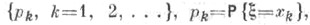 то Э. определяется формулой
то Э. определяется формулой
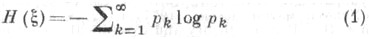
(при этом считается, что 0 log 0=0). Основанием логарифма может служить любое положительное число, но обычно рассматривают логарифмы по основанию 2 или е, что соответствует выбору бит или нат (натуральная единица) в качестве единицы измерения.
Если 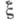 и
и 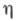 - две дискретные случайные величины, принимающие значения х 1, х2, ... и y1, y2, ... с распределениями вероятностей {pk, k=1, 2, . . .} и {qj, j=1, 2, . . .} соответственно, и {pk|j, k=l, 2, . . .} - условное распределение
- две дискретные случайные величины, принимающие значения х 1, х2, ... и y1, y2, ... с распределениями вероятностей {pk, k=1, 2, . . .} и {qj, j=1, 2, . . .} соответственно, и {pk|j, k=l, 2, . . .} - условное распределение 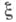 при условии, что
при условии, что 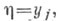 j=1, 2, . . ., то (средней) условной Э.
j=1, 2, . . ., то (средней) условной Э. 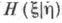 величины
величины  относительно
относительно 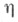 наз. величина
наз. величина
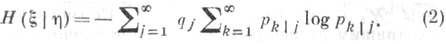
Пусть  - стационарный процесс с дискретным временем и дискретным пространством значений такой, что
- стационарный процесс с дискретным временем и дискретным пространством значений такой, что  Тогда Э. (точнее, средней Э. на символ)
Тогда Э. (точнее, средней Э. на символ)  такого стационарного процесса наз. предел
такого стационарного процесса наз. предел

где 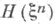 - Э. случайной величины
- Э. случайной величины 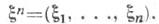 Известно, что предел в правой части (3) всегда существует и имеет место равенство
Известно, что предел в правой части (3) всегда существует и имеет место равенство

где  - условная Э.
- условная Э. относительно
относительно  Э. стационарных процессов находит важные применения в теории динамич. систем.
Э. стационарных процессов находит важные применения в теории динамич. систем.
Если 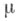 и v - две меры на нек-ром измеримом пространстве
и v - две меры на нек-ром измеримом пространстве 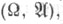 причем мера
причем мера 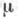 абсолютно непрерывна относительно v и
абсолютно непрерывна относительно v и 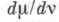 - соответствующая производная Радона - Никодима, то Э.
- соответствующая производная Радона - Никодима, то Э.  меры
меры  относительно меры v наз. интеграл
относительно меры v наз. интеграл

Частным случаем Э. меры по мере является дифференциальная энтропия.
Из многих возможных обобщений понятия Э. для теории информации одним ил самых важных является следующее. Пусть 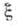 и
и 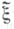 - две случайные величины, принимающие значения в нек-рых измеримых пространствах
- две случайные величины, принимающие значения в нек-рых измеримых пространствах 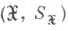 и
и 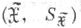 соответственно. Пусть заданы распределение
соответственно. Пусть заданы распределение  случайной величины
случайной величины 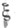 и класс Wдопустимых совместных распределений пары
и класс Wдопустимых совместных распределений пары 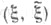 в множестве всех вероятностных мер в произведении
в множестве всех вероятностных мер в произведении  Тогда W-энтропией (или Э. при заданном условии сообщений точности воспроизведения W )наз. величина
Тогда W-энтропией (или Э. при заданном условии сообщений точности воспроизведения W )наз. величина
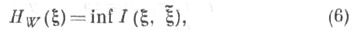
где 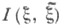 - информации количество в
- информации количество в 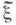 относительно
относительно  а нижняя грань берется по всем парам случайных величин
а нижняя грань берется по всем парам случайных величин  таким, что совместное распределение
таким, что совместное распределение
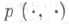 пары
пары  принадлежит W, а
принадлежит W, а 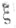 имеет распределение
имеет распределение 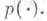 Класс W совместных распределений
Класс W совместных распределений 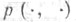 часто задают с помощью нек-рой неотрицательной измеримой действительнозначной функции
часто задают с помощью нек-рой неотрицательной измеримой действительнозначной функции 
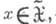 - меры искажения следующим образом:
- меры искажения следующим образом:

где  - нек-рое фиксированное число. В этом случае величину, определяемую равенством (6), где Wзадается (7), называют
- нек-рое фиксированное число. В этом случае величину, определяемую равенством (6), где Wзадается (7), называют 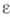 -энтропией (или скоростью как функцией искажения) и обозначают
-энтропией (или скоростью как функцией искажения) и обозначают 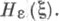 Напр., если
Напр., если 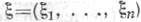 - гауссовский случайный вектор с независимыми компонентами,
- гауссовский случайный вектор с независимыми компонентами, 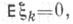 k=1,2, ..., п, а функция
k=1,2, ..., п, а функция 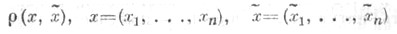 имеет вид
имеет вид
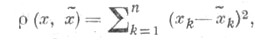
то 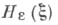 может быть найдена по формуле
может быть найдена по формуле
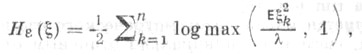 где
где 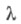 определяется из уравнения
определяется из уравнения 
Если 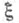 - дискретная случайная величина, пространства
- дискретная случайная величина, пространства  и
и 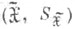 совпадают, а функция
совпадают, а функция  имеет вид
имеет вид

то 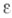 -Э. при
-Э. при 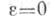 равна обычной Э., определяемой в (1), т. е.
равна обычной Э., определяемой в (1), т. е.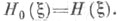
Лит.:[1]Шеннон К., Математическая теория связи, в сб.: Работы по теории информации и кибернетике, пер. с англ., М., 196З, с. 243-332; [2] Галл агер Р., Теория информации и надежная связь, пер. с англ., М., 1974; [3] Berger Т., Rate distortion theory, Englewood Cliffs (N. J.), 1971; [4] Биллингeлeй И., Эргодическая теория и информация, пер. с англ., М., 1969.
Р. Л. Добрушин, В. В. Прелов.

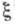 - дискретная случайная величина, определенная на нек-ром вероятностном пространстве
- дискретная случайная величина, определенная на нек-ром вероятностном пространстве  и принимающая значения x1, x2, . . . с распределением вероятностей
и принимающая значения x1, x2, . . . с распределением вероятностей 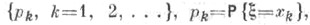 то Э. определяется формулой
то Э. определяется формулой 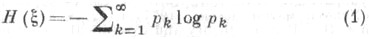
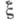 и
и 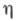 - две дискретные случайные величины, принимающие значения х 1, х2, ... и y1, y2, ... с распределениями вероятностей {pk, k=1, 2, . . .} и {qj, j=1, 2, . . .} соответственно, и {pk|j, k=l, 2, . . .} - условное распределение
- две дискретные случайные величины, принимающие значения х 1, х2, ... и y1, y2, ... с распределениями вероятностей {pk, k=1, 2, . . .} и {qj, j=1, 2, . . .} соответственно, и {pk|j, k=l, 2, . . .} - условное распределение 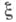 при условии, что
при условии, что 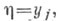 j=1, 2, . . ., то (средней) условной Э.
j=1, 2, . . ., то (средней) условной Э. 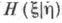 величины
величины  относительно
относительно 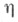 наз. величина
наз. величина 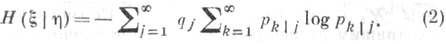
 - стационарный процесс с дискретным временем и дискретным пространством значений такой, что
- стационарный процесс с дискретным временем и дискретным пространством значений такой, что  Тогда Э. (точнее, средней Э. на символ)
Тогда Э. (точнее, средней Э. на символ)  такого стационарного процесса наз. предел
такого стационарного процесса наз. предел 
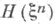 - Э. случайной величины
- Э. случайной величины 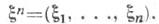 Известно, что предел в правой части (3) всегда существует и имеет место равенство
Известно, что предел в правой части (3) всегда существует и имеет место равенство 
 - условная Э.
- условная Э. относительно
относительно  Э. стационарных процессов находит важные применения в теории динамич. систем.
Э. стационарных процессов находит важные применения в теории динамич. систем. 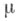 и v - две меры на нек-ром измеримом пространстве
и v - две меры на нек-ром измеримом пространстве 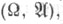 причем мера
причем мера 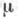 абсолютно непрерывна относительно v и
абсолютно непрерывна относительно v и 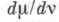 - соответствующая производная Радона - Никодима, то Э.
- соответствующая производная Радона - Никодима, то Э.  меры
меры  относительно меры v наз. интеграл
относительно меры v наз. интеграл 
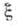 и
и 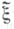 - две случайные величины, принимающие значения в нек-рых измеримых пространствах
- две случайные величины, принимающие значения в нек-рых измеримых пространствах 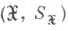 и
и 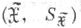 соответственно. Пусть заданы распределение
соответственно. Пусть заданы распределение  случайной величины
случайной величины 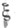 и класс Wдопустимых совместных распределений пары
и класс Wдопустимых совместных распределений пары 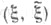 в множестве всех вероятностных мер в произведении
в множестве всех вероятностных мер в произведении  Тогда W-энтропией (или Э. при заданном условии сообщений точности воспроизведения W )наз. величина
Тогда W-энтропией (или Э. при заданном условии сообщений точности воспроизведения W )наз. величина 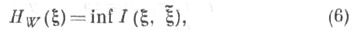
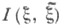 - информации количество в
- информации количество в 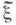 относительно
относительно  а нижняя грань берется по всем парам случайных величин
а нижняя грань берется по всем парам случайных величин  таким, что совместное распределение
таким, что совместное распределение 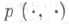 пары
пары  принадлежит W, а
принадлежит W, а 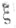 имеет распределение
имеет распределение 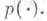 Класс W совместных распределений
Класс W совместных распределений 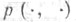 часто задают с помощью нек-рой неотрицательной измеримой действительнозначной функции
часто задают с помощью нек-рой неотрицательной измеримой действительнозначной функции 
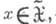 - меры искажения следующим образом:
- меры искажения следующим образом: 
 - нек-рое фиксированное число. В этом случае величину, определяемую равенством (6), где Wзадается (7), называют
- нек-рое фиксированное число. В этом случае величину, определяемую равенством (6), где Wзадается (7), называют 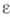 -энтропией (или скоростью как функцией искажения) и обозначают
-энтропией (или скоростью как функцией искажения) и обозначают 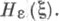 Напр., если
Напр., если 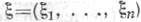 - гауссовский случайный вектор с независимыми компонентами,
- гауссовский случайный вектор с независимыми компонентами, 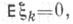 k=1,2, ..., п, а функция
k=1,2, ..., п, а функция 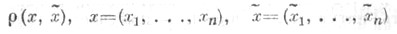 имеет вид
имеет вид 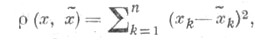
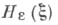 может быть найдена по формуле
может быть найдена по формуле 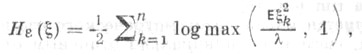 где
где 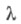 определяется из уравнения
определяется из уравнения 
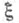 - дискретная случайная величина, пространства
- дискретная случайная величина, пространства  и
и 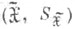 совпадают, а функция
совпадают, а функция  имеет вид
имеет вид 
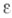 -Э. при
-Э. при 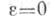 равна обычной Э., определяемой в (1), т. е.
равна обычной Э., определяемой в (1), т. е.