"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭЛЛИПТИЧЕСКИЙ ОПЕРАТОР
Значение ЭЛЛИПТИЧЕСКИЙ ОПЕРАТОР в математической энциклопедии:
-линейный дифференциальный или псевдодифференциальный оператор с обратимым главным символом (см. Символ оператора).
Пусть А- дифференциальный или псевдодифференциальный оператор (вообще говоря, матричный) на области  с главным символом
с главным символом  Если А- оператор порядка т, то
Если А- оператор порядка т, то  -матричная функция на
-матричная функция на  положительно однородная порядка тпо переменному
положительно однородная порядка тпо переменному  Тогда эллиптичность означает, что
Тогда эллиптичность означает, что  -обратимая матрица при всех
-обратимая матрица при всех 
 Это понятие эллиптичности наз. эллиптичностью по Петровскому.
Это понятие эллиптичности наз. эллиптичностью по Петровскому.
Другой вид эллиптичности, эллиптичность по Дуглису - Ниренбергу, предполагает, что А- матричный оператор,  где
где  -оператор порядка sj - ti,(s1,..., sd) и (t1,..., td) - нек-рые наборы действительных чисел. Тогда можно образовать матрицу главных символов
-оператор порядка sj - ti,(s1,..., sd) и (t1,..., td) - нек-рые наборы действительных чисел. Тогда можно образовать матрицу главных символов  где функция
где функция  положительно однородна по
положительно однородна по  порядка sj-ti. Тогда эллиптичность по Дуглису - Ниренбергу означает, что матрица
порядка sj-ti. Тогда эллиптичность по Дуглису - Ниренбергу означает, что матрица  обратима при всех
обратима при всех 
Эллиптичность оператора Ана многообразии означает эллиптичность операторов, к-рые получаются из него при его записи в локальных координатах. Равносильным образом эту эллиптичность можно описать как обратимость главного символа  к-рый является функцией на
к-рый является функцией на  где Т*Х - кокасательное расслоение к
где Т*Х - кокасательное расслоение к  - то же расслоение без нулевого сечения. Если оператор Адействует в сечениях векторных расслоений
- то же расслоение без нулевого сечения. Если оператор Адействует в сечениях векторных расслоений  то эллиптичность оператора означает обратимость линейного оператора
то эллиптичность оператора означает обратимость линейного оператора  для любой точки
для любой точки 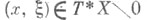 (здесь Е х, Fx- слои расслоений Еи . в точке x). Примером Э. о. является Лапласа оператор.
(здесь Е х, Fx- слои расслоений Еи . в точке x). Примером Э. о. является Лапласа оператор.
Эллиптичность оператора равносильна отсутствию у него действительных характеристич. направлений. Эллиптичность можно также понимать микролокально. А именно, эллиптичность оператора Ав точке  означает обратимость матрицы (линейного отображения)
означает обратимость матрицы (линейного отображения) 
Эллиптичность псевдодифференциального оператора на многообразии с краем (напр., оператора из алгебры Бутеде Монвеля [10], [11]) в граничной точке означает обратимость нек-рого модельного оператора граничной задачи на полуоси. Этот модельный оператор получается из исходного выпрямлением границы, замораживанием коэффициентов главных частей оператора и граничных условий в рассматриваемой точке и взятием преобразования Фурье по касательным направлениям (от  с последующим фиксированием ненулевого вектора
с последующим фиксированием ненулевого вектора  к-рый можно рассматривать как кокаса тельный вектор к границе. В случае дифференциального оператора и дифференциальных граничных условий описанное условие эллиптичности может быть записано в алгебраич. терминах. В этом случае (а также иногда и в общем случае) это условие часто наз. условием Шапиро - Лопатинского, или условием коэрцитивности.
к-рый можно рассматривать как кокаса тельный вектор к границе. В случае дифференциального оператора и дифференциальных граничных условий описанное условие эллиптичности может быть записано в алгебраич. терминах. В этом случае (а также иногда и в общем случае) это условие часто наз. условием Шапиро - Лопатинского, или условием коэрцитивности.
Наиболее характерными свойствами Э. о. являются: 1) свойства регулярности решений соответствующих уравнений; 2) точные априорные оценки; 3) фредгольмовость Э. о. на компактных многообразиях.
Ниже, для простоты, коэффициенты и символы всех операторов считаются бесконечногладкими.
Пусть дано уравнение Au=f, где А - Э. <о. Простейшее свойство регулярности таково: если  то
то  Это свойство верно для любых дифференциальных Э. о. с гладкими коэффициентами или псевдодифференциальных Э. о. (с гладкими символами). Оно верно и для Э. о. краевой задачи (т. е. верно вплоть до границы при выполнении условия Шапиро - Лопатинского). Уточнением этого свойства является его микролокальный вариант: если оператор Аэллиптичен в точке
Это свойство верно для любых дифференциальных Э. о. с гладкими коэффициентами или псевдодифференциальных Э. о. (с гладкими символами). Оно верно и для Э. о. краевой задачи (т. е. верно вплоть до границы при выполнении условия Шапиро - Лопатинского). Уточнением этого свойства является его микролокальный вариант: если оператор Аэллиптичен в точке  (здесь x0- внутренняя точка X)и
(здесь x0- внутренняя точка X)и  то
то  где WF означает фронт волновой (распределения или функции). Другое уточнение: если А- Э. о. порядка ти
где WF означает фронт волновой (распределения или функции). Другое уточнение: если А- Э. о. порядка ти  то
то  где
где  - Соболева пространство,
- Соболева пространство,  Если А - дифференциальный Э. о. с аналитич. оэффициентами, то из аналитичности f вытекает аналитичность и(в случае уравнений с постоянными коэффициентами это свойство необходимо и достаточно для эллиптичности). Соответствующий микролокальный вариант также справедлив и формулируется на языке аналитических волновых фронтов.
Если А - дифференциальный Э. о. с аналитич. оэффициентами, то из аналитичности f вытекает аналитичность и(в случае уравнений с постоянными коэффициентами это свойство необходимо и достаточно для эллиптичности). Соответствующий микролокальный вариант также справедлив и формулируется на языке аналитических волновых фронтов.
Локальная априорная оценка для Э. о. . порядка тимеет вид

где  и
и  - две области в
- две области в  причем
причем  - компакт, принадлежащий
- компакт, принадлежащий  Au=f в
Au=f в  постоянная Сне зависит от и(но может зависеть от
постоянная Сне зависит от и(но может зависеть от 
Глобальная априорная оценка для Э. о. . порядка тна компактном многообразии Xбез края имеет тот же вид, что и (1), но с заменой  и
и  на X. В случае многообразия с краем вместо норм пространств
на X. В случае многообразия с краем вместо норм пространств  в (1) нужно взять нормы, учитывающие структуру вектор-функций ии f (содержащих, вообще говоря, граничные компоненты). Напр., пусть на компактном многообразии X с краем Yзадан Э. о. вида
в (1) нужно взять нормы, учитывающие структуру вектор-функций ии f (содержащих, вообще говоря, граничные компоненты). Напр., пусть на компактном многообразии X с краем Yзадан Э. о. вида  где А -- эллиптический дифференциальный оператор порядка т, В j - дифференциальные операторы порядков mj, причем mj<m и выполнено условие Шапиро - Лопатинского (для оператора Аи системы граничных операторов B1, . . ., В r). Тогда априорная оценка в пространствах Соболева
где А -- эллиптический дифференциальный оператор порядка т, В j - дифференциальные операторы порядков mj, причем mj<m и выполнено условие Шапиро - Лопатинского (для оператора Аи системы граничных операторов B1, . . ., В r). Тогда априорная оценка в пространствах Соболева  имеет вид
имеет вид

где  - норма в пространстве
- норма в пространстве  - норма в пространстве
- норма в пространстве  и постоянная С>0 не зависит от и(но может зависеть от A, Bj, s, X, Y и выбора норм в пространствах Соболева).
и постоянная С>0 не зависит от и(но может зависеть от A, Bj, s, X, Y и выбора норм в пространствах Соболева).
Э. о. на компактном многообразии (возможно, с краем) определяет фредгольмов оператор в соответствующих соболевских пространствах, а также в пространствах бесконечно дифференцируемых функций. Его индекс зависит лишь от главного символа и не меняется при непрерывных деформациях главного символа. Это позволяет поставить вопрос о вычислении индекса (см. Индекса формулы).
Важную роль играют Э. о. с параметром (см. [12]). При выполнении условия эллиптичности с параметром на компактном многообразии при больших по модулю значениях параметра рассматриваемый Э. о. оказывается обратимым, причем в глобальной априорной оценке типа (1) можно опустить последний член (младшую норму и в правой части).
Лит.:[1] Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; [2] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [3] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, М., 1973; [4] Лионс Ж. Л., Мадженес Э., Неоднородные граничные задачи и их приложения, пер. с франц., М., 1971; [5] Берс Л., Джон Ф., Шехтер М., Уравнения с частными производными, пер. с англ., М., 1966; [6] Агмон С., Дуглис А., Ниренберг Л., Оценки вблизи границы решений эллиптических уравнений в частных производных при общих граничных условиях, пер. с англ., М., 1962; [7] Хермандер Л., Линейные дифференциальные операторы с частными производными, пер. с англ., М., 1965; [8] Шубин М. А., Псевдодифференциальные операторы и спектральная теория, М., 1978; [9] Палей Р., Семинар по теореме Атьи-Зингера об индексе, пер. с англ., М., 1970; [10] Rempel S., Schulze В. W., Index theory of elliptic boundary problems, В., 1982; [11] Boutet de Monvel L., лActa main..

 с главным символом
с главным символом  Если А- оператор порядка т, то
Если А- оператор порядка т, то  -матричная функция на
-матричная функция на  положительно однородная порядка тпо переменному
положительно однородная порядка тпо переменному  Тогда эллиптичность означает, что
Тогда эллиптичность означает, что  -обратимая матрица при всех
-обратимая матрица при всех 
 Это понятие эллиптичности наз. эллиптичностью по Петровскому.
Это понятие эллиптичности наз. эллиптичностью по Петровскому.  где
где  -оператор порядка sj - ti,(s1,..., sd) и (t1,..., td) - нек-рые наборы действительных чисел. Тогда можно образовать матрицу главных символов
-оператор порядка sj - ti,(s1,..., sd) и (t1,..., td) - нек-рые наборы действительных чисел. Тогда можно образовать матрицу главных символов  где функция
где функция  положительно однородна по
положительно однородна по  порядка sj-ti. Тогда эллиптичность по Дуглису - Ниренбергу означает, что матрица
порядка sj-ti. Тогда эллиптичность по Дуглису - Ниренбергу означает, что матрица  обратима при всех
обратима при всех 
 к-рый является функцией на
к-рый является функцией на  где Т*Х - кокасательное расслоение к
где Т*Х - кокасательное расслоение к  - то же расслоение без нулевого сечения. Если оператор Адействует в сечениях векторных расслоений
- то же расслоение без нулевого сечения. Если оператор Адействует в сечениях векторных расслоений  то эллиптичность оператора означает обратимость линейного оператора
то эллиптичность оператора означает обратимость линейного оператора  для любой точки
для любой точки 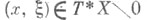 (здесь Е х, Fx- слои расслоений Еи . в точке x). Примером Э. о. является Лапласа оператор.
(здесь Е х, Fx- слои расслоений Еи . в точке x). Примером Э. о. является Лапласа оператор.  означает обратимость матрицы (линейного отображения)
означает обратимость матрицы (линейного отображения) 
 с последующим фиксированием ненулевого вектора
с последующим фиксированием ненулевого вектора  к-рый можно рассматривать как кокаса тельный вектор к границе. В случае дифференциального оператора и дифференциальных граничных условий описанное условие эллиптичности может быть записано в алгебраич. терминах. В этом случае (а также иногда и в общем случае) это условие часто наз. условием Шапиро - Лопатинского, или условием коэрцитивности.
к-рый можно рассматривать как кокаса тельный вектор к границе. В случае дифференциального оператора и дифференциальных граничных условий описанное условие эллиптичности может быть записано в алгебраич. терминах. В этом случае (а также иногда и в общем случае) это условие часто наз. условием Шапиро - Лопатинского, или условием коэрцитивности.  то
то  Это свойство верно для любых дифференциальных Э. о. с гладкими коэффициентами или псевдодифференциальных Э. о. (с гладкими символами). Оно верно и для Э. о. краевой задачи (т. е. верно вплоть до границы при выполнении условия Шапиро - Лопатинского). Уточнением этого свойства является его микролокальный вариант: если оператор Аэллиптичен в точке
Это свойство верно для любых дифференциальных Э. о. с гладкими коэффициентами или псевдодифференциальных Э. о. (с гладкими символами). Оно верно и для Э. о. краевой задачи (т. е. верно вплоть до границы при выполнении условия Шапиро - Лопатинского). Уточнением этого свойства является его микролокальный вариант: если оператор Аэллиптичен в точке  (здесь x0- внутренняя точка X)и
(здесь x0- внутренняя точка X)и  то
то  где WF означает фронт волновой (распределения или функции). Другое уточнение: если А- Э. о. порядка ти
где WF означает фронт волновой (распределения или функции). Другое уточнение: если А- Э. о. порядка ти  то
то  где
где  - Соболева пространство,
- Соболева пространство,  Если А - дифференциальный Э. о. с аналитич. оэффициентами, то из аналитичности f вытекает аналитичность и(в случае уравнений с постоянными коэффициентами это свойство необходимо и достаточно для эллиптичности). Соответствующий микролокальный вариант также справедлив и формулируется на языке аналитических волновых фронтов.
Если А - дифференциальный Э. о. с аналитич. оэффициентами, то из аналитичности f вытекает аналитичность и(в случае уравнений с постоянными коэффициентами это свойство необходимо и достаточно для эллиптичности). Соответствующий микролокальный вариант также справедлив и формулируется на языке аналитических волновых фронтов. 
 и
и  - две области в
- две области в  причем
причем  - компакт, принадлежащий
- компакт, принадлежащий  Au=f в
Au=f в  постоянная Сне зависит от и(но может зависеть от
постоянная Сне зависит от и(но может зависеть от 
 и
и  на X. В случае многообразия с краем вместо норм пространств
на X. В случае многообразия с краем вместо норм пространств  в (1) нужно взять нормы, учитывающие структуру вектор-функций ии f (содержащих, вообще говоря, граничные компоненты). Напр., пусть на компактном многообразии X с краем Yзадан Э. о. вида
в (1) нужно взять нормы, учитывающие структуру вектор-функций ии f (содержащих, вообще говоря, граничные компоненты). Напр., пусть на компактном многообразии X с краем Yзадан Э. о. вида  где А -- эллиптический дифференциальный оператор порядка т, В j - дифференциальные операторы порядков mj, причем mj<m и выполнено условие Шапиро - Лопатинского (для оператора Аи системы граничных операторов B1, . . ., В r). Тогда априорная оценка в пространствах Соболева
где А -- эллиптический дифференциальный оператор порядка т, В j - дифференциальные операторы порядков mj, причем mj<m и выполнено условие Шапиро - Лопатинского (для оператора Аи системы граничных операторов B1, . . ., В r). Тогда априорная оценка в пространствах Соболева  имеет вид
имеет вид 
 - норма в пространстве
- норма в пространстве  - норма в пространстве
- норма в пространстве  и постоянная С>0 не зависит от и(но может зависеть от A, Bj, s, X, Y и выбора норм в пространствах Соболева).
и постоянная С>0 не зависит от и(но может зависеть от A, Bj, s, X, Y и выбора норм в пространствах Соболева).