"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
Значение ЭЛЕМЕНТАРНАЯ ТЕОРИЯ в математической энциклопедии:
- совокупность замкнутых формул логики предикатов 1-й ступени. Э. т. Th(К) класса К алгебраических систем сигнатуры  наз. совокупность всех замкнутых формул логики предикатов 1-й ступени сигнатуры
наз. совокупность всех замкнутых формул логики предикатов 1-й ступени сигнатуры  истинных на всех системах из класса К. Если класс Ксостоит из одной системы А, то Э. т. класса Кназ. Э. т. системы А. Две алгебраич. системы одной сигнатуры наз. элементарно эквивалентными, если их Э. т. совпадают. Алгебраич. система Асигнатуры
истинных на всех системах из класса К. Если класс Ксостоит из одной системы А, то Э. т. класса Кназ. Э. т. системы А. Две алгебраич. системы одной сигнатуры наз. элементарно эквивалентными, если их Э. т. совпадают. Алгебраич. система Асигнатуры  наз. моделью Э. т. Тсигнатуры
наз. моделью Э. т. Тсигнатуры  если все формулы из Тистинны в А. Э. т. наз. совместной, если она имеет модели. Совместная Э. т. наз. полной, если любые две ее модели элементарно эквивалентны. Класс всех моделей Э. т. Т обозначается Mod(Т). Э. т. Тназ. разрешимой, если множество формул Th(Mod(Т)) (т. е. совокупность всех логич. следствий из Т)рекурсивно. Класс . алгебраич. систем сигнатуры
если все формулы из Тистинны в А. Э. т. наз. совместной, если она имеет модели. Совместная Э. т. наз. полной, если любые две ее модели элементарно эквивалентны. Класс всех моделей Э. т. Т обозначается Mod(Т). Э. т. Тназ. разрешимой, если множество формул Th(Mod(Т)) (т. е. совокупность всех логич. следствий из Т)рекурсивно. Класс . алгебраич. систем сигнатуры  наз. аксиоматизируемым, если существует такая Э. т. Тсигнатуры
наз. аксиоматизируемым, если существует такая Э. т. Тсигнатуры  что К=Mod(Т). В этом случае Тназ. совокупностью аксиом для К. Класс Ктогда и только тогда аксиоматизируем, когда К=Mod(Th(К)). Напр., класс плотно линейно упорядоченных множеств без наименьшего и наибольшего элементов аксиоматизируем, его Э. т. разрешима, любые две системы из этого класса элементарно эквивалентны, значит Э. т. этого класса полна; кроме того. Э. т. рассматриваемого класса конечно аксиоматизируема. Класс конечных циклич. групп не является аксиоматизируемым, однако его Э. т. разрешима и, значит, рекурсивно аксиоматизируема. Имеются примеры конечно аксиоматизируемых неразрешимых Э. т. Такими являются Э. т. групп, колец, полей и др. Однако полная рекурсивно аксиоматизируемая Э. т. обязательно разрешима. Поэтому для доказательства разрешимости рекурсивно аксиоматизируемой Э. т. достаточно заметить, что эта Э. т. полна.
что К=Mod(Т). В этом случае Тназ. совокупностью аксиом для К. Класс Ктогда и только тогда аксиоматизируем, когда К=Mod(Th(К)). Напр., класс плотно линейно упорядоченных множеств без наименьшего и наибольшего элементов аксиоматизируем, его Э. т. разрешима, любые две системы из этого класса элементарно эквивалентны, значит Э. т. этого класса полна; кроме того. Э. т. рассматриваемого класса конечно аксиоматизируема. Класс конечных циклич. групп не является аксиоматизируемым, однако его Э. т. разрешима и, значит, рекурсивно аксиоматизируема. Имеются примеры конечно аксиоматизируемых неразрешимых Э. т. Такими являются Э. т. групп, колец, полей и др. Однако полная рекурсивно аксиоматизируемая Э. т. обязательно разрешима. Поэтому для доказательства разрешимости рекурсивно аксиоматизируемой Э. т. достаточно заметить, что эта Э. т. полна.
Известен ряд методов доказательства полноты. Э. т. наз. категоричной в мощности  если все ее модели мощности
если все ее модели мощности  изоморфны. Э. т., категоричная в нек-рой бесконечной мощности и не имеющая конечных моделей, обязательно полна. Напр., Э. т. алгебраически замкнутых полей фиксированной характеристики рекурсивно аксиоматизируема и категорична в каждой несчетной мощности, а конечных моделей не имеет, поэтому эта теория полна и разрешима. В частности, разрешима Э. т. поля комплексных чисел. Две формулы той же сигнатуры, что и сигнатура теории Т, эквивалентны в теории Т, если эти формулы имеют одинаковые свободные переменные и для любой модели Атеории Ти любого способа приписывания этим свободным переменным элементов модели Алибо обе формулы одновременно истинны при этих значениях неизвестных, либо обе они ложны. Полная Э. т. Тконечной или счетной сигнатуры тогда и только тогда счетно категорична, когда для каждого псуществует конечное число формул с псвободными переменными v1, . . ., vn такое, что каждая формула соответствующей сигнатуры со свободными переменными vl, ... ., vn аквивалентна в Тодной из этих формул. Полная теория конечной или счетной сигнатуры, категоричная в одной несчетной мощности, категорична и во всякой другой несчетной мощности. Система Асигнатуры
изоморфны. Э. т., категоричная в нек-рой бесконечной мощности и не имеющая конечных моделей, обязательно полна. Напр., Э. т. алгебраически замкнутых полей фиксированной характеристики рекурсивно аксиоматизируема и категорична в каждой несчетной мощности, а конечных моделей не имеет, поэтому эта теория полна и разрешима. В частности, разрешима Э. т. поля комплексных чисел. Две формулы той же сигнатуры, что и сигнатура теории Т, эквивалентны в теории Т, если эти формулы имеют одинаковые свободные переменные и для любой модели Атеории Ти любого способа приписывания этим свободным переменным элементов модели Алибо обе формулы одновременно истинны при этих значениях неизвестных, либо обе они ложны. Полная Э. т. Тконечной или счетной сигнатуры тогда и только тогда счетно категорична, когда для каждого псуществует конечное число формул с псвободными переменными v1, . . ., vn такое, что каждая формула соответствующей сигнатуры со свободными переменными vl, ... ., vn аквивалентна в Тодной из этих формул. Полная теория конечной или счетной сигнатуры, категоричная в одной несчетной мощности, категорична и во всякой другой несчетной мощности. Система Асигнатуры  наз. элементарной подсистемой системы Втой же сигнатуры, если Аявляется подсистемой системы Ви для всякой формулы Ф(v1, . . ., vn) логики предикатов 1-й ступени сигнатура
наз. элементарной подсистемой системы Втой же сигнатуры, если Аявляется подсистемой системы Ви для всякой формулы Ф(v1, . . ., vn) логики предикатов 1-й ступени сигнатура  со свободными переменными v1, . . ., vn и всяких а 1, . . .,
со свободными переменными v1, . . ., vn и всяких а 1, . . .,  из истинности Ф(а 1, . . . ., а n) в . следует истинность Ф(а 1, . . . ., а n) в Д. Э. т. Тназ. модельно полной, если для любых ее моделей . и Виз того, что Аявляется подсистемой системы В, следует, что Аявляется элементарной подсистемой В, Оказывается, что модeльно полная теория, имеющая такую модель, к-рая изоморфно вкладывается во всякую модель этой теории, является полной. Универсально эквивалентными наз. такие алгебраич. системы одной сигнатуры, на к-рых истинны одни и те же предваренные формулы, не содержащие кванторов существования. Модельно полная Э. т., все модели к-рой универсально эквивалентны, является полной. Используя технику модельной полноты, можно доказать полноту и разрешимость Э. т. вещественно замкнутых полей, в частности поля действительных чисел. Среди других Э. т., являющихся разрешимыми. - Э. т. сложения целых и натуральных чисел, Э. т. абелевых групп, поля р-адических чисел, конечных нолей, нолей вычетов, упорядоченных абелевых групп, булевых алгебр.
из истинности Ф(а 1, . . . ., а n) в . следует истинность Ф(а 1, . . . ., а n) в Д. Э. т. Тназ. модельно полной, если для любых ее моделей . и Виз того, что Аявляется подсистемой системы В, следует, что Аявляется элементарной подсистемой В, Оказывается, что модeльно полная теория, имеющая такую модель, к-рая изоморфно вкладывается во всякую модель этой теории, является полной. Универсально эквивалентными наз. такие алгебраич. системы одной сигнатуры, на к-рых истинны одни и те же предваренные формулы, не содержащие кванторов существования. Модельно полная Э. т., все модели к-рой универсально эквивалентны, является полной. Используя технику модельной полноты, можно доказать полноту и разрешимость Э. т. вещественно замкнутых полей, в частности поля действительных чисел. Среди других Э. т., являющихся разрешимыми. - Э. т. сложения целых и натуральных чисел, Э. т. абелевых групп, поля р-адических чисел, конечных нолей, нолей вычетов, упорядоченных абелевых групп, булевых алгебр.
Теория неразрешимых Э. т. была заложена А. Тарским (A. Tarski) в 40-е гг. 20 в., хотя неразрешимость логики предикатов первой ступени была доказана А. Чёрчем (A. Church) еще в 1936, а неразрешимость арифметики натуральных чисел - Дж. Россером (J. Rosser) также в 1936. Говорят, что Э. т. Th (К) класса Калгебраич. систем одной сигнатуры  неотделима, если не существует рекурсивного множества формул, содержащего все тождественно истинные замкнутые формулы сигнатуры
неотделима, если не существует рекурсивного множества формул, содержащего все тождественно истинные замкнутые формулы сигнатуры  и содержащегося в Th(К). Э. т. класса К 1 систем сигнатуры
и содержащегося в Th(К). Э. т. класса К 1 систем сигнатуры  состоящей из одного двуместного предиката, наз. относительно определимой в Э. <т. класса К 2 систем сигнатуры
состоящей из одного двуместного предиката, наз. относительно определимой в Э. <т. класса К 2 систем сигнатуры  если существуют такие формулы
если существуют такие формулы 
 сигнатуры
сигнатуры  что для каждой системы А 1 из K1 можно найти такую систему А 2 из К 2 и такие элементы b1, . . ., bs в А2,что множество
что для каждой системы А 1 из K1 можно найти такую систему А 2 из К 2 и такие элементы b1, . . ., bs в А2,что множество 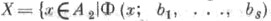 истинно в А 2} вместе с предикатом Р (2), определенным на Xтак, что
истинно в А 2} вместе с предикатом Р (2), определенным на Xтак, что 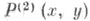 истинно тогда и только тогда, когда
истинно тогда и только тогда, когда 
 истинно в А 2, образует алгебраич. систему, изоморфную системе А 1.Это определение естественным образом распространяется и на теории классов К 1 произвольной сигнатуры. Если неотделимая Э. т. класса K1 относительно определима в Э. т. класса K2. то Э. т. класса K2 тоже неотделима. Это позволяет доказывать неотделимость Э. т. многих классов алгебраич. систем. В качестве Th(K1) при этом удобно брать Э. т. всех конечных бинарных предикатов, Э. т. конечных симметричных предикатов и подобные Э. т. Неотделимые Э. т. неразрешимы. К неразрешимым Э. т. относятся также Э. т. поля рациональных чисел, многих классов колец и полей. Важен результат А. И. Мальцева о неразрешимости Э. т. конечных групп.
истинно в А 2, образует алгебраич. систему, изоморфную системе А 1.Это определение естественным образом распространяется и на теории классов К 1 произвольной сигнатуры. Если неотделимая Э. т. класса K1 относительно определима в Э. т. класса K2. то Э. т. класса K2 тоже неотделима. Это позволяет доказывать неотделимость Э. т. многих классов алгебраич. систем. В качестве Th(K1) при этом удобно брать Э. т. всех конечных бинарных предикатов, Э. т. конечных симметричных предикатов и подобные Э. т. Неотделимые Э. т. неразрешимы. К неразрешимым Э. т. относятся также Э. т. поля рациональных чисел, многих классов колец и полей. Важен результат А. И. Мальцева о неразрешимости Э. т. конечных групп.
Лит.:[1] Ершов Ю. Л., [и др.] лУспехи матем. наук

 наз. совокупность всех замкнутых формул логики предикатов 1-й ступени сигнатуры
наз. совокупность всех замкнутых формул логики предикатов 1-й ступени сигнатуры  истинных на всех системах из класса К. Если класс Ксостоит из одной системы А, то Э. т. класса Кназ. Э. т. системы А. Две алгебраич. системы одной сигнатуры наз. элементарно эквивалентными, если их Э. т. совпадают. Алгебраич. система Асигнатуры
истинных на всех системах из класса К. Если класс Ксостоит из одной системы А, то Э. т. класса Кназ. Э. т. системы А. Две алгебраич. системы одной сигнатуры наз. элементарно эквивалентными, если их Э. т. совпадают. Алгебраич. система Асигнатуры  наз. моделью Э. т. Тсигнатуры
наз. моделью Э. т. Тсигнатуры  если все формулы из Тистинны в А. Э. т. наз. совместной, если она имеет модели. Совместная Э. т. наз. полной, если любые две ее модели элементарно эквивалентны. Класс всех моделей Э. т. Т обозначается Mod(Т). Э. т. Тназ. разрешимой, если множество формул Th(Mod(Т)) (т. е. совокупность всех логич. следствий из Т)рекурсивно. Класс . алгебраич. систем сигнатуры
если все формулы из Тистинны в А. Э. т. наз. совместной, если она имеет модели. Совместная Э. т. наз. полной, если любые две ее модели элементарно эквивалентны. Класс всех моделей Э. т. Т обозначается Mod(Т). Э. т. Тназ. разрешимой, если множество формул Th(Mod(Т)) (т. е. совокупность всех логич. следствий из Т)рекурсивно. Класс . алгебраич. систем сигнатуры  наз. аксиоматизируемым, если существует такая Э. т. Тсигнатуры
наз. аксиоматизируемым, если существует такая Э. т. Тсигнатуры  что К=Mod(Т). В этом случае Тназ. совокупностью аксиом для К. Класс Ктогда и только тогда аксиоматизируем, когда К=Mod(Th(К)). Напр., класс плотно линейно упорядоченных множеств без наименьшего и наибольшего элементов аксиоматизируем, его Э. т. разрешима, любые две системы из этого класса элементарно эквивалентны, значит Э. т. этого класса полна; кроме того. Э. т. рассматриваемого класса конечно аксиоматизируема. Класс конечных циклич. групп не является аксиоматизируемым, однако его Э. т. разрешима и, значит, рекурсивно аксиоматизируема. Имеются примеры конечно аксиоматизируемых неразрешимых Э. т. Такими являются Э. т. групп, колец, полей и др. Однако полная рекурсивно аксиоматизируемая Э. т. обязательно разрешима. Поэтому для доказательства разрешимости рекурсивно аксиоматизируемой Э. т. достаточно заметить, что эта Э. т. полна.
что К=Mod(Т). В этом случае Тназ. совокупностью аксиом для К. Класс Ктогда и только тогда аксиоматизируем, когда К=Mod(Th(К)). Напр., класс плотно линейно упорядоченных множеств без наименьшего и наибольшего элементов аксиоматизируем, его Э. т. разрешима, любые две системы из этого класса элементарно эквивалентны, значит Э. т. этого класса полна; кроме того. Э. т. рассматриваемого класса конечно аксиоматизируема. Класс конечных циклич. групп не является аксиоматизируемым, однако его Э. т. разрешима и, значит, рекурсивно аксиоматизируема. Имеются примеры конечно аксиоматизируемых неразрешимых Э. т. Такими являются Э. т. групп, колец, полей и др. Однако полная рекурсивно аксиоматизируемая Э. т. обязательно разрешима. Поэтому для доказательства разрешимости рекурсивно аксиоматизируемой Э. т. достаточно заметить, что эта Э. т. полна.  если все ее модели мощности
если все ее модели мощности  изоморфны. Э. т., категоричная в нек-рой бесконечной мощности и не имеющая конечных моделей, обязательно полна. Напр., Э. т. алгебраически замкнутых полей фиксированной характеристики рекурсивно аксиоматизируема и категорична в каждой несчетной мощности, а конечных моделей не имеет, поэтому эта теория полна и разрешима. В частности, разрешима Э. т. поля комплексных чисел. Две формулы той же сигнатуры, что и сигнатура теории Т, эквивалентны в теории Т, если эти формулы имеют одинаковые свободные переменные и для любой модели Атеории Ти любого способа приписывания этим свободным переменным элементов модели Алибо обе формулы одновременно истинны при этих значениях неизвестных, либо обе они ложны. Полная Э. т. Тконечной или счетной сигнатуры тогда и только тогда счетно категорична, когда для каждого псуществует конечное число формул с псвободными переменными v1, . . ., vn такое, что каждая формула соответствующей сигнатуры со свободными переменными vl, ... ., vn аквивалентна в Тодной из этих формул. Полная теория конечной или счетной сигнатуры, категоричная в одной несчетной мощности, категорична и во всякой другой несчетной мощности. Система Асигнатуры
изоморфны. Э. т., категоричная в нек-рой бесконечной мощности и не имеющая конечных моделей, обязательно полна. Напр., Э. т. алгебраически замкнутых полей фиксированной характеристики рекурсивно аксиоматизируема и категорична в каждой несчетной мощности, а конечных моделей не имеет, поэтому эта теория полна и разрешима. В частности, разрешима Э. т. поля комплексных чисел. Две формулы той же сигнатуры, что и сигнатура теории Т, эквивалентны в теории Т, если эти формулы имеют одинаковые свободные переменные и для любой модели Атеории Ти любого способа приписывания этим свободным переменным элементов модели Алибо обе формулы одновременно истинны при этих значениях неизвестных, либо обе они ложны. Полная Э. т. Тконечной или счетной сигнатуры тогда и только тогда счетно категорична, когда для каждого псуществует конечное число формул с псвободными переменными v1, . . ., vn такое, что каждая формула соответствующей сигнатуры со свободными переменными vl, ... ., vn аквивалентна в Тодной из этих формул. Полная теория конечной или счетной сигнатуры, категоричная в одной несчетной мощности, категорична и во всякой другой несчетной мощности. Система Асигнатуры  наз. элементарной подсистемой системы Втой же сигнатуры, если Аявляется подсистемой системы Ви для всякой формулы Ф(v1, . . ., vn) логики предикатов 1-й ступени сигнатура
наз. элементарной подсистемой системы Втой же сигнатуры, если Аявляется подсистемой системы Ви для всякой формулы Ф(v1, . . ., vn) логики предикатов 1-й ступени сигнатура  со свободными переменными v1, . . ., vn и всяких а 1, . . .,
со свободными переменными v1, . . ., vn и всяких а 1, . . .,  из истинности Ф(а 1, . . . ., а n) в . следует истинность Ф(а 1, . . . ., а n) в Д. Э. т. Тназ. модельно полной, если для любых ее моделей . и Виз того, что Аявляется подсистемой системы В, следует, что Аявляется элементарной подсистемой В, Оказывается, что модeльно полная теория, имеющая такую модель, к-рая изоморфно вкладывается во всякую модель этой теории, является полной. Универсально эквивалентными наз. такие алгебраич. системы одной сигнатуры, на к-рых истинны одни и те же предваренные формулы, не содержащие кванторов существования. Модельно полная Э. т., все модели к-рой универсально эквивалентны, является полной. Используя технику модельной полноты, можно доказать полноту и разрешимость Э. т. вещественно замкнутых полей, в частности поля действительных чисел. Среди других Э. т., являющихся разрешимыми. - Э. т. сложения целых и натуральных чисел, Э. т. абелевых групп, поля р-адических чисел, конечных нолей, нолей вычетов, упорядоченных абелевых групп, булевых алгебр.
из истинности Ф(а 1, . . . ., а n) в . следует истинность Ф(а 1, . . . ., а n) в Д. Э. т. Тназ. модельно полной, если для любых ее моделей . и Виз того, что Аявляется подсистемой системы В, следует, что Аявляется элементарной подсистемой В, Оказывается, что модeльно полная теория, имеющая такую модель, к-рая изоморфно вкладывается во всякую модель этой теории, является полной. Универсально эквивалентными наз. такие алгебраич. системы одной сигнатуры, на к-рых истинны одни и те же предваренные формулы, не содержащие кванторов существования. Модельно полная Э. т., все модели к-рой универсально эквивалентны, является полной. Используя технику модельной полноты, можно доказать полноту и разрешимость Э. т. вещественно замкнутых полей, в частности поля действительных чисел. Среди других Э. т., являющихся разрешимыми. - Э. т. сложения целых и натуральных чисел, Э. т. абелевых групп, поля р-адических чисел, конечных нолей, нолей вычетов, упорядоченных абелевых групп, булевых алгебр.  неотделима, если не существует рекурсивного множества формул, содержащего все тождественно истинные замкнутые формулы сигнатуры
неотделима, если не существует рекурсивного множества формул, содержащего все тождественно истинные замкнутые формулы сигнатуры  и содержащегося в Th(К). Э. т. класса К 1 систем сигнатуры
и содержащегося в Th(К). Э. т. класса К 1 систем сигнатуры  состоящей из одного двуместного предиката, наз. относительно определимой в Э. <т. класса К 2 систем сигнатуры
состоящей из одного двуместного предиката, наз. относительно определимой в Э. <т. класса К 2 систем сигнатуры  если существуют такие формулы
если существуют такие формулы 
 сигнатуры
сигнатуры  что для каждой системы А 1 из K1 можно найти такую систему А 2 из К 2 и такие элементы b1, . . ., bs в А2,что множество
что для каждой системы А 1 из K1 можно найти такую систему А 2 из К 2 и такие элементы b1, . . ., bs в А2,что множество 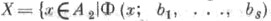 истинно в А 2} вместе с предикатом Р (2), определенным на Xтак, что
истинно в А 2} вместе с предикатом Р (2), определенным на Xтак, что 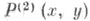 истинно тогда и только тогда, когда
истинно тогда и только тогда, когда 
 истинно в А 2, образует алгебраич. систему, изоморфную системе А 1.Это определение естественным образом распространяется и на теории классов К 1 произвольной сигнатуры. Если неотделимая Э. т. класса K1 относительно определима в Э. т. класса K2. то Э. т. класса K2 тоже неотделима. Это позволяет доказывать неотделимость Э. т. многих классов алгебраич. систем. В качестве Th(K1) при этом удобно брать Э. т. всех конечных бинарных предикатов, Э. т. конечных симметричных предикатов и подобные Э. т. Неотделимые Э. т. неразрешимы. К неразрешимым Э. т. относятся также Э. т. поля рациональных чисел, многих классов колец и полей. Важен результат А. И. Мальцева о неразрешимости Э. т. конечных групп.
истинно в А 2, образует алгебраич. систему, изоморфную системе А 1.Это определение естественным образом распространяется и на теории классов К 1 произвольной сигнатуры. Если неотделимая Э. т. класса K1 относительно определима в Э. т. класса K2. то Э. т. класса K2 тоже неотделима. Это позволяет доказывать неотделимость Э. т. многих классов алгебраич. систем. В качестве Th(K1) при этом удобно брать Э. т. всех конечных бинарных предикатов, Э. т. конечных симметричных предикатов и подобные Э. т. Неотделимые Э. т. неразрешимы. К неразрешимым Э. т. относятся также Э. т. поля рациональных чисел, многих классов колец и полей. Важен результат А. И. Мальцева о неразрешимости Э. т. конечных групп.