"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭЛЕМЕНТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ
Значение ЭЛЕМЕНТ АНАЛИТИЧЕСКОЙ ФУНКЦИИ в математической энциклопедии:
совокупность (D, f) области Dна плоскости комплексного переменного  и аналитич. ции f(z), заданной в Dпри помощи нек-рого аналитич. аппарата, позволяющего эффективно осуществить аналитич. родолжение f(z) во всю ее область существования как полной аналитической функции. Наиболее простой и чаще всего применяемой формой Э. а. ф. является круговой элемент в виде совокупности степенного ряда
и аналитич. ции f(z), заданной в Dпри помощи нек-рого аналитич. аппарата, позволяющего эффективно осуществить аналитич. родолжение f(z) во всю ее область существования как полной аналитической функции. Наиболее простой и чаще всего применяемой формой Э. а. ф. является круговой элемент в виде совокупности степенного ряда

и его круга сходимости  с центром а(центр элемента) и радиусом сходимости R>0. Аналитич. продолжение здесь достигается (быть может, многократным) переразложением ряда (1) для различных центров
с центром а(центр элемента) и радиусом сходимости R>0. Аналитич. продолжение здесь достигается (быть может, многократным) переразложением ряда (1) для различных центров  по формулам вида
по формулам вида

Любой из элементов (D, f) полной аналитич. ции определяет ее однозначно и может быть представлен посредством круговых элементов с центрами  В случае бесконечно удаленного центра
В случае бесконечно удаленного центра  круговой элемент принимает вид
круговой элемент принимает вид  с областью сходимости
с областью сходимости 
В процессе аналитич. родолжения функция f(z) может оказаться многозначной и могут появиться соответствующие алгебраическим точкам ветвления т. н. разветвленные элементы вида

где v>l, число v-1 наз. порядком разветвленности. Разветвленные элементы обобщают понятие Э. а, ф., последние в этой связи наа. также неразветвленными (при v=l) регулярными  элементами.
элементами.
В качестве простейшего элемента (D, f )аналитич. функции f(z) многих комплексных переменных  |
|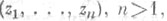 можно принять совокупность кратного степенного ряда
можно принять совокупность кратного степенного ряда
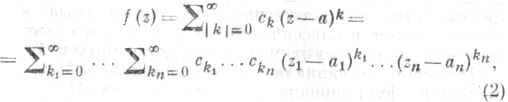
где a=(al,. . ., а n) - центр, 
 и нек-рого поликруга
и нек-рого поликруга
 в к-ром ряд (2) абсолютно сходится. Однако, при п> 1 следует иметь в виду, что поликруг не является точной областью абсолютной сходимости степенного ряди.
в к-ром ряд (2) абсолютно сходится. Однако, при п> 1 следует иметь в виду, что поликруг не является точной областью абсолютной сходимости степенного ряди.
Понятие Э. а. ф. весьма близко к понятию ростка аналитич. функции.
Лит.:[1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1-2, М., 1967-68; [2] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964.
E. Д. Соломенцев.

 и аналитич. ции f(z), заданной в Dпри помощи нек-рого аналитич. аппарата, позволяющего эффективно осуществить аналитич. родолжение f(z) во всю ее область существования как полной аналитической функции. Наиболее простой и чаще всего применяемой формой Э. а. ф. является круговой элемент в виде совокупности степенного ряда
и аналитич. ции f(z), заданной в Dпри помощи нек-рого аналитич. аппарата, позволяющего эффективно осуществить аналитич. родолжение f(z) во всю ее область существования как полной аналитической функции. Наиболее простой и чаще всего применяемой формой Э. а. ф. является круговой элемент в виде совокупности степенного ряда 
 с центром а(центр элемента) и радиусом сходимости R>0. Аналитич. продолжение здесь достигается (быть может, многократным) переразложением ряда (1) для различных центров
с центром а(центр элемента) и радиусом сходимости R>0. Аналитич. продолжение здесь достигается (быть может, многократным) переразложением ряда (1) для различных центров  по формулам вида
по формулам вида 
 В случае бесконечно удаленного центра
В случае бесконечно удаленного центра  круговой элемент принимает вид
круговой элемент принимает вид  с областью сходимости
с областью сходимости 

 элементами.
элементами.  |
|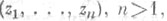 можно принять совокупность кратного степенного ряда
можно принять совокупность кратного степенного ряда 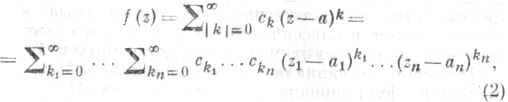

 и нек-рого поликруга
и нек-рого поликруга  в к-ром ряд (2) абсолютно сходится. Однако, при п> 1 следует иметь в виду, что поликруг не является точной областью абсолютной сходимости степенного ряди.
в к-ром ряд (2) абсолютно сходится. Однако, при п> 1 следует иметь в виду, что поликруг не является точной областью абсолютной сходимости степенного ряди.