"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭКСЦЕССА КОЭФФИЦИЕНТ
Значение ЭКСЦЕССА КОЭФФИЦИЕНТ в математической энциклопедии:
, эксцесс,- скалярная характеристика островершинности графика плотности вероятности унимодального распределения, к-рую используют в качестве нек-рой меры отклонения рассматриваемого распределения от нормального. Э. к.  определяется по формуле
определяется по формуле

где  есть 2-й коэффициент Пирсона,
есть 2-й коэффициент Пирсона,  и
и  - 2-й и 4-й центральные моменты вероятностного распределения. В терминах семиинвариантов (кумулянтов)
- 2-й и 4-й центральные моменты вероятностного распределения. В терминах семиинвариантов (кумулянтов)  и
и  второго и четвертого порядков Э. к. имеет вид
второго и четвертого порядков Э. к. имеет вид

Если  то говорят, что плотность вероятности распределения имеет нормальный эксцесс, ибо для нормального распределения Э. к.
то говорят, что плотность вероятности распределения имеет нормальный эксцесс, ибо для нормального распределения Э. к.  В случае, если Э. к.
В случае, если Э. к.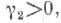 то говорят, что плотность вероятности имеет положительный эксцесс, что, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. В случае, когда
то говорят, что плотность вероятности имеет положительный эксцесс, что, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. В случае, когда  говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона.
говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона.
Если X1, X2, . ..., Х п - независимые случайные величины, подчиняющиеся одному и тому же непрерывному вероятностному закону, то статистика

наз. выборочным коэффициентом эксцесса, где

Выборочный Э. к. используется и качестве точечной статистич. оценки Э. к.
используется и качестве точечной статистич. оценки Э. к.  когда закон распределения случайной величины Xi неизвестен. В случае нормальной распределенности случайных величин X1, . . ., Х n выборочный Э. к.
когда закон распределения случайной величины Xi неизвестен. В случае нормальной распределенности случайных величин X1, . . ., Х n выборочный Э. к.  асимптотически нормально распределен при
асимптотически нормально распределен при  с параметрами
с параметрами

и

Именно поэтому, если наблюденное значение выборочного Э. к.  существенно отличается от 0, то следует признать, что распределение случайной величины Xi отлично от нормального, чем и пользуются на практике при проверке гипотезы
существенно отличается от 0, то следует признать, что распределение случайной величины Xi отлично от нормального, чем и пользуются на практике при проверке гипотезы  принятие к-рой равносильно признанию отклонения распределения случайной величины Xi от нормального.
принятие к-рой равносильно признанию отклонения распределения случайной величины Xi от нормального.
Лит.:[1] Кендалл М. Дж., Стьюарт А., Теория распределений, пер. с англ., М., 1966; [2] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; [3] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 3 изд., М., 1983.
М. С. Никулин.

 определяется по формуле
определяется по формуле 
 есть 2-й коэффициент Пирсона,
есть 2-й коэффициент Пирсона,  и
и  - 2-й и 4-й центральные моменты вероятностного распределения. В терминах семиинвариантов (кумулянтов)
- 2-й и 4-й центральные моменты вероятностного распределения. В терминах семиинвариантов (кумулянтов)  и
и  второго и четвертого порядков Э. к. имеет вид
второго и четвертого порядков Э. к. имеет вид 
 то говорят, что плотность вероятности распределения имеет нормальный эксцесс, ибо для нормального распределения Э. к.
то говорят, что плотность вероятности распределения имеет нормальный эксцесс, ибо для нормального распределения Э. к.  В случае, если Э. к.
В случае, если Э. к.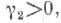 то говорят, что плотность вероятности имеет положительный эксцесс, что, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. В случае, когда
то говорят, что плотность вероятности имеет положительный эксцесс, что, как правило, соответствует тому, что график плотности рассматриваемого распределения в окрестности моды имеет более острую и более высокую вершину, чем нормальная кривая. В случае, когда  говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона.
говорят об отрицательном эксцессе плотности, при этом плотность вероятности имеет в окрестности моды более низкую и плоскую вершину, чем плотность нормального закона. 

 используется и качестве точечной статистич. оценки Э. к.
используется и качестве точечной статистич. оценки Э. к.  когда закон распределения случайной величины Xi неизвестен. В случае нормальной распределенности случайных величин X1, . . ., Х n выборочный Э. к.
когда закон распределения случайной величины Xi неизвестен. В случае нормальной распределенности случайных величин X1, . . ., Х n выборочный Э. к.  асимптотически нормально распределен при
асимптотически нормально распределен при  с параметрами
с параметрами 

 существенно отличается от 0, то следует признать, что распределение случайной величины Xi отлично от нормального, чем и пользуются на практике при проверке гипотезы
существенно отличается от 0, то следует признать, что распределение случайной величины Xi отлично от нормального, чем и пользуются на практике при проверке гипотезы  принятие к-рой равносильно признанию отклонения распределения случайной величины Xi от нормального.
принятие к-рой равносильно признанию отклонения распределения случайной величины Xi от нормального.