"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ
Значение ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ в математической энциклопедии:
численные методы решения - методы вычислительной математики, применяемые для поиска экстремумов (максимумов или минимумов) функций и функционалов.
Для численного решения экстремальных задач, рассматриваемых в бесконечномерных функциональных пространствах (напр., задач оптимального управления процессами, описываемыми обыкновенными дифференциальными уравнениями или уравнениями с частными производными) могут быть использованы после соответствующего обобщения многие методы математич. программирования, разработанные для задач минимизации или максимизации функций конечного числа неременных. При этом в конкретных задачах весьма важен правильный выбор подходящего функционального пространства, в к-ром следует ее рассматривать. При выборе такого пространства обычно учитываются физич. соображения, свойства допустимых управлений, свойства решений соответствующих начально-краевых задач при фиксированном управлении и т. п.
Напр., задачу оптимального управления, заключающуюся в минимизации функционала

при условиях

часто бывает удобнорассматривать вфункциональном пространстве  Здесь х=(x1, . . . х n), и=(u1, . . . , ur), f=(f1, . . . , fn), fi(x, и, t), i=0, 1, ... , n, F (х) - заданные функции; t0, Т- известные моменты времени, t0<T; х0 - заданная начальная точка; V(t)при каждом
Здесь х=(x1, . . . х n), и=(u1, . . . , ur), f=(f1, . . . , fn), fi(x, и, t), i=0, 1, ... , n, F (х) - заданные функции; t0, Т- известные моменты времени, t0<T; х0 - заданная начальная точка; V(t)при каждом 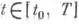 - заданное множество из евклидова пространства
- заданное множество из евклидова пространства  - гильбертово пространство r-мерных вектор-функций
- гильбертово пространство r-мерных вектор-функций 
 где
где  - функция, интегрируемая на [t0, Т] по Лебегу вместе со своим квадратом
- функция, интегрируемая на [t0, Т] по Лебегу вместе со своим квадратом  причем скалярное произведение двух функций u(t), v(t), в этом пространстве равно
причем скалярное произведение двух функций u(t), v(t), в этом пространстве равно

норма

При определенной гладкости функций f' ( х, и, t), F(x)приращение функционала (1) можно представить в виде

где

x=x(f, u)- решение задачи (2) при u=u(t),  -решение сопряженной задачи
-решение сопряженной задачи

Из формулы (4) следует, чтр функционал (1) дифференцируем в пространстве  и его градиентом является вектор-функция
и его градиентом является вектор-функция
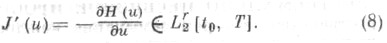
Таким образом, для решения задачи (1) - (3) могут быть применены различные методы, использующие градиент функционала. При V(t)=Er здесь можно применить градиентный метод

Если 
 где
где  - заданные функции из
- заданные функции из 
 то возможно применение метода проекции градиента
то возможно применение метода проекции градиента

где

Параметр  может выбираться из условия
может выбираться из условия 
 Аналогично могут быть расписаны для задачи (1)-(3) методы условного градиента, сопряженных градиентов и др. (см.[4]-[6],[11]). Еслизадача(1)-(3) рассматривается при дополнительных ограничениях
Аналогично могут быть расписаны для задачи (1)-(3) методы условного градиента, сопряженных градиентов и др. (см.[4]-[6],[11]). Еслизадача(1)-(3) рассматривается при дополнительных ограничениях

где G(t)- заданное множество из Е n, то для учета ограничений (9) может быть использован штрафных функций метод. Напр., если

то в качестве штрафной функции можно взять

и задачу (1)-(3), (9) заменить задачей минимизации функционала Ф k(u)=J(u)+AkP (и)при условиях (2), (3), где Ak, -штрафной коэффициент, 
Другие методы решения задачи (1)-(3), (9) основаны на принципе максимума Понтрягина, на динамич. программировании (см. Понтрягина принцип максимума, Динамическое программирование, Вариационное исчисление;численные методы).
Для решения задачи минимизации квадратичного функционала на решениях систем линейных обыкновенных дифференциальных уравнений или линейных уравнений с частными производными, может быть применен метод моментов (см. [3], [8]). Ниже описан этот метод применительно к задаче минимизации функционала

где х-=х(t; и) - решение задачи

управления  таковы, что
таковы, что

здесь A(t), B(t), f(t)-заданные матрицы порядка  соответственно, имеющие кусочно непрерывные элементы на отрезке
соответственно, имеющие кусочно непрерывные элементы на отрезке 
 - заданные точки;
- заданные точки; 
 -скалярное произведение в Е т. Из правила множителей Лагранжа следует, что управление и=и(t)является оптимальным в задаче (10)-(12) тогда и только тогда, когда существует число
-скалярное произведение в Е т. Из правила множителей Лагранжа следует, что управление и=и(t)является оптимальным в задаче (10)-(12) тогда и только тогда, когда существует число  ( Лагранжа множитель для ограничения (12)) такое, что
( Лагранжа множитель для ограничения (12)) такое, что

при  здесь
здесь  Из формул (5)-(8) следует, что градиент J'(u)функционала (10) в
Из формул (5)-(8) следует, что градиент J'(u)функционала (10) в 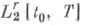 имеет вид
имеет вид

где  - решение задачи
- решение задачи

А Т, В Т- матрицы, полученные транспонированием матриц А, В соответственно. Условие (13) тогда примет вид

Условие (16) равносильно соотношениям

где

р k(t) - решение системы (15) при условии pk(T)=ek=(0, ... ,0, 1, 0, ... , 0) - единичный вектор.
Таким образом, для определения оптимального управления u=u(t) в задаче (10)-(12) нужно решить систему (14), (15), (17), (18) относительно функций  и числа
и числа  При
При  здесь
здесь  . и условие (18) приведет к проблеме моментов (см. Моментов про6лема):
. и условие (18) приведет к проблеме моментов (см. Моментов про6лема):
найти функцию u-=u(t), зная ее моменты
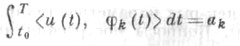
по системе  k=1, .... , n. Система (14), (15), (17), (18) представляет собой обобщенную проблему моментов для задачи (10) - (12) при
k=1, .... , n. Система (14), (15), (17), (18) представляет собой обобщенную проблему моментов для задачи (10) - (12) при  (см. [3], [8]).
(см. [3], [8]).
Любое решение  системы (15) однозначно представимо в виде
системы (15) однозначно представимо в виде

При любом фиксированном  существует решение
существует решение  системы (15), (17), (18), причем среди всех решений найдется единственное такое, что
системы (15), (17), (18), причем среди всех решений найдется единственное такое, что  имеет вид
имеет вид

Для определения  нужно подставить выражения (19), (20) в (17), (18). В результате получится система линейных алгебраических уравнении относительно
нужно подставить выражения (19), (20) в (17), (18). В результате получится система линейных алгебраических уравнении относительно  u1, . . ., и n, из к-рой однозначно определяются величины
u1, . . ., и n, из к-рой однозначно определяются величины  а величины u1, ... , и n в случае линейной зависимости системы
а величины u1, ... , и n в случае линейной зависимости системы  определяются неоднозначно.
определяются неоднозначно.
При практич. решении задачи (10)-(12) целесообразно сначала положить 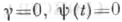 и из (18) определить u(t,0) вида (20). Затем следует проверить условие
и из (18) определить u(t,0) вида (20). Затем следует проверить условие  Если это неравенство выполняется, то u(f,0) - оптимальное управление задачи (10)-(12), имеющее минимальную норму среди всех оптимальных управлений; множество всех оптимальных управлений в этом случае исчерпывается управлениями вида
Если это неравенство выполняется, то u(f,0) - оптимальное управление задачи (10)-(12), имеющее минимальную норму среди всех оптимальных управлений; множество всех оптимальных управлений в этом случае исчерпывается управлениями вида

где v(t)принадлежит ортогональному дополнению в  линейной оболочки систем функций
линейной оболочки систем функций

Если  то из (17), (18) при
то из (17), (18) при  определяют решения
определяют решения  вида (19), (20) и находят g из уравнения
вида (19), (20) и находят g из уравнения

функция  переменной
переменной  непрерывна, строго монотонно убывает при
непрерывна, строго монотонно убывает при  поэтому из (21) однозначно определяется искомое
поэтому из (21) однозначно определяется искомое  Управление
Управление  будет оптимальным для задачи (10)-(12); при
будет оптимальным для задачи (10)-(12); при  эта задача других оптимальных управлений не имеет.
эта задача других оптимальных управлений не имеет.
Метод моментов применим также для решения задачи быстродействия для систем (11) и других линейных систем (см. [3], [8]).
Упомянутые выше методы широко используются и для численного решения задач оптимального управления процессами, описываемыми уравнениями с частными производными.
Численная реализация многих методов решения задач оптимального управления предполагает использование тех или иных методов приближенного решения встречающихся начально-краевых задач (см. Краевая задача;численные методы решения для уравнений с частными производными), приближенного вычисления интегралов (см. Интегрирование численное). В результате исходная задача оптимального управления заменяется нек-рым семейством аппроксимирующих задач, зависящим от нек-рых параметров (напр., от шагов разностной сетки). Вопросы построения аппроксимирующих задач, исследование сходимости см. в [5].
Широкие классы экстремальных задач являются некорректно поставленными (см. Некорректные задачи )и для их решения нужно использовать регуляризации методы (см. [5], [13]).
Лит.:[1] Алексеев В. М., Тихомиров В. М., Фомин С. В., Оптимальное управление, М., 1979; [2] Бейко И. В., Бублик Б. Н., 3инько П. Н., Методы и алгоритмы решения задач оптимизации, К., 1983; [3] Бутковский А. Г., Методы управления системами с распределенными параметрами, М., 1975; [4] Васильев Ф. П., Численные методы решения экстремальных задач, М., 1980; [5] его же, Методы решения экстремальных задач, М., 1981; [6] Евтушенко Ю. Г., Методы решения экстремальных задач и их применение в системах оптимизации, М., 1982; [7] Егоров А. И., Оптимальное управление тепловыми и диффузионными процессами, М., 1978; [8] Красовский Н. Н., Теория управления движением, М., 1968; [9] Лионс Ж.-Л., Оптимальное управление системами, описываемыми уравнениями с частными производными, пер. с франц., М., 1972; [10] Поляк Б. Т., Введение в оптимизацию, М., 1983; [11] Cea Ж., Оптимизация. Теория и алгоритмы, пер. с франц., М., 1973; [12] Сиразeтдинов Т. К., Оптимизация систем с распределенными параметрами, М., 1977; [13] Тихонов А. Н., Арсeнин В. Я.. Методы решения некорректных задач, 2 изд., М., 1979; [14] Федоренко Р. П., Приближенное решение задач оптимального управления, М., 1978; [15] Экланд П., Темам Р., Выпуклый анализ и вариационные проблемы, пер. с англ., М., 1979.
Ф. П. Васильев.



 Здесь х=(x1, . . . х n), и=(u1, . . . , ur), f=(f1, . . . , fn), fi(x, и, t), i=0, 1, ... , n, F (х) - заданные функции; t0, Т- известные моменты времени, t0<T; х0 - заданная начальная точка; V(t)при каждом
Здесь х=(x1, . . . х n), и=(u1, . . . , ur), f=(f1, . . . , fn), fi(x, и, t), i=0, 1, ... , n, F (х) - заданные функции; t0, Т- известные моменты времени, t0<T; х0 - заданная начальная точка; V(t)при каждом 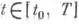 - заданное множество из евклидова пространства
- заданное множество из евклидова пространства  - гильбертово пространство r-мерных вектор-функций
- гильбертово пространство r-мерных вектор-функций 
 где
где  - функция, интегрируемая на [t0, Т] по Лебегу вместе со своим квадратом
- функция, интегрируемая на [t0, Т] по Лебегу вместе со своим квадратом  причем скалярное произведение двух функций u(t), v(t), в этом пространстве равно
причем скалярное произведение двух функций u(t), v(t), в этом пространстве равно 



 -решение сопряженной задачи
-решение сопряженной задачи 
 и его градиентом является вектор-функция
и его градиентом является вектор-функция 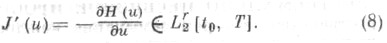


 где
где  - заданные функции из
- заданные функции из 
 то возможно применение метода проекции градиента
то возможно применение метода проекции градиента 

 может выбираться из условия
может выбираться из условия 
 Аналогично могут быть расписаны для задачи (1)-(3) методы условного градиента, сопряженных градиентов и др. (см.[4]-[6],[11]). Еслизадача(1)-(3) рассматривается при дополнительных ограничениях
Аналогично могут быть расписаны для задачи (1)-(3) методы условного градиента, сопряженных градиентов и др. (см.[4]-[6],[11]). Еслизадача(1)-(3) рассматривается при дополнительных ограничениях 





 таковы, что
таковы, что 
 соответственно, имеющие кусочно непрерывные элементы на отрезке
соответственно, имеющие кусочно непрерывные элементы на отрезке 
 - заданные точки;
- заданные точки; 
 -скалярное произведение в Е т. Из правила множителей Лагранжа следует, что управление и=и(t)является оптимальным в задаче (10)-(12) тогда и только тогда, когда существует число
-скалярное произведение в Е т. Из правила множителей Лагранжа следует, что управление и=и(t)является оптимальным в задаче (10)-(12) тогда и только тогда, когда существует число  ( Лагранжа множитель для ограничения (12)) такое, что
( Лагранжа множитель для ограничения (12)) такое, что 
 здесь
здесь  Из формул (5)-(8) следует, что градиент J'(u)функционала (10) в
Из формул (5)-(8) следует, что градиент J'(u)функционала (10) в 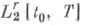 имеет вид
имеет вид 
 - решение задачи
- решение задачи 



 и числа
и числа  При
При  здесь
здесь  . и условие (18) приведет к проблеме моментов (см. Моментов про6лема):
. и условие (18) приведет к проблеме моментов (см. Моментов про6лема): 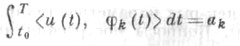
 k=1, .... , n. Система (14), (15), (17), (18) представляет собой обобщенную проблему моментов для задачи (10) - (12) при
k=1, .... , n. Система (14), (15), (17), (18) представляет собой обобщенную проблему моментов для задачи (10) - (12) при  (см. [3], [8]).
(см. [3], [8]).  системы (15) однозначно представимо в виде
системы (15) однозначно представимо в виде 
 существует решение
существует решение  системы (15), (17), (18), причем среди всех решений найдется единственное такое, что
системы (15), (17), (18), причем среди всех решений найдется единственное такое, что  имеет вид
имеет вид 
 нужно подставить выражения (19), (20) в (17), (18). В результате получится система линейных алгебраических уравнении относительно
нужно подставить выражения (19), (20) в (17), (18). В результате получится система линейных алгебраических уравнении относительно  u1, . . ., и n, из к-рой однозначно определяются величины
u1, . . ., и n, из к-рой однозначно определяются величины  а величины u1, ... , и n в случае линейной зависимости системы
а величины u1, ... , и n в случае линейной зависимости системы  определяются неоднозначно.
определяются неоднозначно. 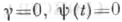 и из (18) определить u(t,0) вида (20). Затем следует проверить условие
и из (18) определить u(t,0) вида (20). Затем следует проверить условие  Если это неравенство выполняется, то u(f,0) - оптимальное управление задачи (10)-(12), имеющее минимальную норму среди всех оптимальных управлений; множество всех оптимальных управлений в этом случае исчерпывается управлениями вида
Если это неравенство выполняется, то u(f,0) - оптимальное управление задачи (10)-(12), имеющее минимальную норму среди всех оптимальных управлений; множество всех оптимальных управлений в этом случае исчерпывается управлениями вида 
 линейной оболочки систем функций
линейной оболочки систем функций 
 то из (17), (18) при
то из (17), (18) при  определяют решения
определяют решения  вида (19), (20) и находят g из уравнения
вида (19), (20) и находят g из уравнения 
 переменной
переменной  непрерывна, строго монотонно убывает при
непрерывна, строго монотонно убывает при  поэтому из (21) однозначно определяется искомое
поэтому из (21) однозначно определяется искомое  Управление
Управление  будет оптимальным для задачи (10)-(12); при
будет оптимальным для задачи (10)-(12); при  эта задача других оптимальных управлений не имеет.
эта задача других оптимальных управлений не имеет.