"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭКСПОНЕНЦИАЛЬНОЕ ОТОБРАЖЕНИЕЗначение ЭКСПОНЕНЦИАЛЬНОЕ ОТОБРАЖЕНИЕ в математической энциклопедии:
отображение касательного пространства многообразия Мв М, определяемое заданной на М связностью и являющееся далеко идущим обобщением обычной экспоненциальной функции, рассматриваемой как отображение прямой в себя.
1) Пусть М - многообразие класса 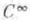 с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из 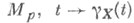 - геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение - геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение  является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если  и и 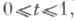 то то 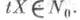 В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка 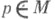 обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М. обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.
2)Пусть G- группа Ли с единицей еи g - соответствующая алгебра Ли, состоящая из касательных векторов к G в точке е. Для каждого вектора  существует единственный аналитич. омоморфизм существует единственный аналитич. омоморфизм 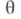 группы группы 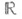 в Gтакой, что касательный вектор к в Gтакой, что касательный вектор к 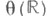 в точке есовпадает с X. Отображение в точке есовпадает с X. Отображение  и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение 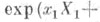  есть система координат на Ne, эти координаты наз. каноническими. есть система координат на Ne, эти координаты наз. каноническими.
К понятию Э. о. для группы Ли G можно подойти и с другой точки зрения. Существует взаимно однозначное соответствие между множеством всех аффинных связностей на G, инвариантных относительно группы левых сдвигов, и множеством билинейных функций 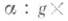  Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции  Лит.:[1] Xелгасoн С., Дифференциальная геометрия и симметрические пространства, пер. с англ., М., 1964.
А. С. Феденко.
|

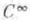 с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из
с аффинной связностью, р - нек-рая точка из М, М р - касательное пространство к многообразию Мв точке ри X - ненулевой вектор из 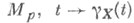 - геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение
- геодезическая, проходящая через точку р в направлении вектора X. Существует такая открытая окрестность N0 точки 0 в М р и такая открытая окрестность N р точки рв М, что отображение  является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если
является диффеоморфизмом N0 на N р. Это отображение называется Э. о. в точке р и обозначается Ехр. Окрестность N0 наз. нормальной, если: 1) отображение Ехр диффеоморфно отображает N0 на N р,2) если  и
и 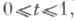 то
то 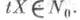 В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка
В этом случае N р - нормальная окрестность точки . в многообразии М. Каждая точка 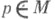 обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.
обладает выпуклой нормальной окрестностью N р точки р: любые две точки такой окрестности можно соединить в точности одним геодезич. отрезком, содержащимся в N р. Если М - полное риманово многообразие, то Ехр есть сюръективное отображение М р на М.  существует единственный аналитич. омоморфизм
существует единственный аналитич. омоморфизм 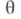 группы
группы 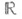 в Gтакой, что касательный вектор к
в Gтакой, что касательный вектор к 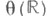 в точке есовпадает с X. Отображение
в точке есовпадает с X. Отображение  и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение
и наз. Э. о. алгебры gв группу G. Существует такая открытая окрестность N0 точки 0 в gи такая открытая окрестность N е точки ев G, что ехр является аналитич. диффеоморфизмом окрестности N0 на Ne. Пусть Х 1, ... , Х п - нек-рый базис алгебры g. Отображение 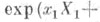
 есть система координат на Ne, эти координаты наз. каноническими.
есть система координат на Ne, эти координаты наз. каноническими. 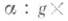
 Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции
Оказывается, что Э. о. ехр алгебры gв группу G совпадают с отображением Ехр касательного пространства gк многообразию . в точке ев это многообразие относительно лсвоинвариантной аффинной связности, отвечающей любой кососимметричной билинейной функции 