"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АВТОРЕГРЕССИОННЫЙ ПРОЦЕССЗначение АВТОРЕГРЕССИОННЫЙ ПРОЦЕСС в математической энциклопедии:
случайный процесс  значения к-рого удовлетворяют при нек-рых постоянных значения к-рого удовлетворяют при нек-рых постоянных 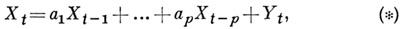 
уравнению авторегрессии где р - нек-рое положительное число, а величины  обычно предполагаются некоррелированными и одинаково распределенными со средним 0 и дисперсией обычно предполагаются некоррелированными и одинаково распределенными со средним 0 и дисперсией  Если все нули функции Если все нули функции  комплексного аргумента комплексного аргумента  лежат внутри единичного круга, уравнение лежат внутри единичного круга, уравнение 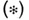 имеет решение имеет решение

где  связаны с связаны с 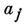 соотношением соотношением

Пусть, напр.,  является процессом белого шума со спектральной плотностью является процессом белого шума со спектральной плотностью  ; тогда единственным А. п., удовлетворяющим уравнению ; тогда единственным А. п., удовлетворяющим уравнению  , будет стационарный в широком смысле процесс , будет стационарный в широком смысле процесс  со спектральной плотностью со спектральной плотностью  если если  не имеет действительных нулей. Автоковариации процесса не имеет действительных нулей. Автоковариации процесса  удовлетворяют рекуррентному соотношению удовлетворяют рекуррентному соотношению

и в терминах  имеют вид имеют вид

Параметры  авторегрессии связаны с коэффициентами автокорреляции процесса авторегрессии связаны с коэффициентами автокорреляции процесса  матричным соотношением матричным соотношением 
где  - матрица коэффициентов автокорреляции (уравнение Юна - Уокера). - матрица коэффициентов автокорреляции (уравнение Юна - Уокера).
Лит.:[1] Grenander U., Rosenblatt M., Statistical analysis of stationary time series, Stockh., 1956; [2] Xeннан Э., Анализ временных рядов, пер. с англ., М., 1964.
А. В. Прохоров.
|

 значения к-рого удовлетворяют при нек-рых постоянных
значения к-рого удовлетворяют при нек-рых постоянных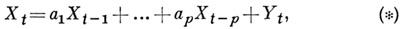

 обычно предполагаются некоррелированными и одинаково распределенными со средним 0 и дисперсией
обычно предполагаются некоррелированными и одинаково распределенными со средним 0 и дисперсией  Если все нули функции
Если все нули функции  комплексного аргумента
комплексного аргумента  лежат внутри единичного круга, уравнение
лежат внутри единичного круга, уравнение 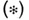 имеет решение
имеет решение 
 связаны с
связаны с 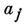 соотношением
соотношением 
 является процессом белого шума со спектральной плотностью
является процессом белого шума со спектральной плотностью  ; тогда единственным А. п., удовлетворяющим уравнению
; тогда единственным А. п., удовлетворяющим уравнению  , будет стационарный в широком смысле процесс
, будет стационарный в широком смысле процесс  со спектральной плотностью
со спектральной плотностью  если
если  не имеет действительных нулей. Автоковариации процесса
не имеет действительных нулей. Автоковариации процесса  удовлетворяют рекуррентному соотношению
удовлетворяют рекуррентному соотношению 
 имеют вид
имеют вид 
 авторегрессии связаны с коэффициентами автокорреляции процесса
авторегрессии связаны с коэффициентами автокорреляции процесса  матричным соотношением
матричным соотношением
 - матрица коэффициентов автокорреляции (уравнение Юна - Уокера).
- матрица коэффициентов автокорреляции (уравнение Юна - Уокера).