|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭЙЛЕРА - МАКЛОРЕНА ФОРМУЛАЗначение ЭЙЛЕРА - МАКЛОРЕНА ФОРМУЛА в математической энциклопедии: формула суммирования, связывающая частные суммы ряда с интегралом и производными его общего члена:
где
Для n=2sостаточный член R2s может быть представлен с использованием чисел Бернулли:
Если производные
Если, кроме того,
то Э.-М. ф. может быть записана в виде:
В такой форме Э. - М. ф. применяется, напр., при выводе Стирлинга формулы. В этом случае
Э.-М. ф. играет важную роль при изучении асимптотич. разложений, в теоретико-числовых оценках, в конечных разностей исчислении.
Э.-М. ф. была впервые приведена Л. Эйлером [1] в виде:
Лит.:[1] Еnlеr L., лComment Acad. sci. Imp. Petrop.
|
|
|
|


 - Бернулли числа, Rn - остаточный член. С помощью Бернулли многочленов Bn(t), В n(0)=В п остаточный член записывается в виде:
- Бернулли числа, Rn - остаточный член. С помощью Бернулли многочленов Bn(t), В n(0)=В п остаточный член записывается в виде: 

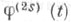 и
и  имеют одинаковые знаки и не меняют знака на [ р, т],то
имеют одинаковые знаки и не меняют знака на [ р, т],то 


 и с - Эйлера постоянная. Имеются обобщения Э. - М. ф. на случай кратных сумм.
и с - Эйлера постоянная. Имеются обобщения Э. - М. ф. на случай кратных сумм.  Э.-М. ф. дает следующее выражение:
Э.-М. ф. дает следующее выражение: 


