|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕЗначение ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ в математической энциклопедии: численные методы - раздел вычислительной математики, посвященный методам отыскания экстремальных значений функционалов. Численные методы В. и. принято разделять на два больших класса: непрямые и прямые методы. Непрямые методы основаны на использовании необходимых условий оптимальности (см. Вариационное исчисление, Эйлера уравнение, Вейерштрасса условия, Трансверсальности условие, Понтрягина принцип максимума), с помощью к-рых исходная вариационная задача сводится к краевой задаче. Поэтому вычислительные достоинства и недостатки непрямых методов полностью определяются свойствами соответствующей краевой задачи. Прямые методы ориентированы на непосредственное отыскание экстремума функционала. Используемые при этом методы оптимизации являются развитием идей математнч. программирования. Разделение численных методов В. и. на прямые и непрямые весьма условно. Нек-рые алгоритмы используют элементы обоих подходов. Кроме того, существуют методы, к-рые непосредственно не относятся к двум выделенным классам. Например, методы, основанные на достаточных условиях оптимальности, образуют самостоятельную группу. Первые численные методы В. и. появились в работах Л. Эйлера (L. Euler). Однако наибольшее развитие они получили с 50-х гг. 20 в. в результате распространения вычислительной техники и открывшейся в связи с этим возможностью решения сложных технич. задач. При этом разработка численных методов В. и. шла в основном применительно к задачам теории оптимального управления - наиболее важного для практич. приложений раздела В. и. (см. Оптимального управления математическая теория). Непрямые методы. С появлением принципа максимума Понтрягина (1956) сведение вариационных задач к краевым стало особенно популярным. Пусть в задаче оптимального управления требуется найти траекторию при дифференциальных связях: граничных условиях: и ограничениях на управление: где Согласно принципу максимума Понтрягина, оптимальное управление где Из условия (6) находится управление Наиболее распространенной схемой численного решения этой краевой задачи является схема, использующая метод Ньютона с дроблением шага (см. [3]). При этом вводится вектор невязки где значение
Решение системы (9) проводится Ньютона методом;используемые при этом частные производные определяются численно по формуле где значения Для определения частных производных известен более точный, но громоздкий метод (см. [4]), в к-ром используется интегрирование системы 2n уравнений в вариациях для системы (2), (7). Трудности в использовании метода Ньютона связаны, во-первых, с проблемой выбора удачного начального приближения для В тех случаях, когда граничные условия и функционал заданы в более общем виде, чем в (3), (4) и (1) [напр., Больца задача с подвижными концами, вариационная задача со свободными (подвижными) концами], к необходимым условиям оптимальности (6), (7) добавляются трансверсальности условия. После исключения входящих в эти условия произвольных постоянных получаются замкнутая краевая задача и отвечающая ей система уравнений типа (9). Решение системы (9) может отыскиваться любым другим методом, применяемым для решения нелинейных систем. Специфич. методы разработаны для решения краевых задач частного вида. Так, линейные краевые задачи решаются методом переноса граничных условий (прогонки метод). Этот метод также используется в качестве составного элемента для итеративного решения .нелинейных краевых задач (см. [1]). Эффективность и относительная простота реализации непрямых методов на ЭВМ сделали их весьма распространенным средством для решения задач вариационного исчисления. Однако эти методы не стали универсальными: для некоторых важных классов задач В. и., например, содержащих фазовые ограничения, выписывание необходимых условий оптимальности затруднено и приводит к краевым задачам со сложной структурой. Кроме того, необходимые условия не гарантируют, что найденное решение доставляет относительный экстремум функционалу. Для проверки приходится привлекать достаточные условия оптимальности. Все это ограничивает сферу применения непрямых методов. Прямые методы. Первый прямой метод был предложен Л. Эйлером для решения простейшей задачи В. и. Этот метод известен под названием метода ломаных Эйлера (или конечно разностного метода Эйлера) и заключается в том, что функционал рассматривается на непрерывных ломаных x(t), удовлетворяющих заданным граничным условиям и состоящих из Nпрямолинейных отрезков с заданными абсциссами концов. Таким образом, функционал превращается в функцию от ординат вершин этих ломаных, а исходная задача - в задачу минимизации функции многих переменных (см. Эйлера метод). Из-за сложности подобных задач для ручного счета прямые методы долгое время оставались в стороне от традиционных исследований по В. и. Интерес к ним вновь возрос в нач. 20 в. Были предложены новые способы редукции к задаче об отыскании экстремума функции многих переменных. Наиболее важным из них является Ритца метод, согласно к-рому решение задачи о минимуме (10) при условии (11) разыскивается на классе функций вида где Задача сводится к отысканию минимума функции Nпеременных
Метод Ритца является достаточно общим. Он применяется для решения вариационных задач математич. физики, заключающихся в минимизации функционала, зависящего от функций многих переменных. Его дальнейшим обобщением для данного класса задач является метод (см. [2]), в к-ром коэффициенты считаются неизвестными функциями одного из независимых переменных (напр., если в задаче две независимые переменные tи Потребности практики увеличили интерес к неклас-сич. задачам оптимального управления. Наличие в технич. задачах сложных ограничений на фазовые координаты и управляющие функции, разрывность правых частей дифференциальных уравнений, возможность существования особых и скользящих оптимальных режимов и т. д.- все это потребовало разработки новых разновидностей прямых методов. Наибольшее распространение получили методы, использующие идеи спуска в пространстве управлений и идеи последовательного анализа вариантов (типа динамического программирования). Методы спуска в пространстве управлений основаны на получении последовательности управлений к-рой соответствует монотонно убывающая последовательность значений функционала. Пусть, напр., ищется минимум функционала при условиях (2), (3) и (5) (U - выпуклое и односвяз-ное множество). Отыскание линейная часть приращения функционала (13) от вариации
Для уменьшения функционала (13) следует на каждой итерации выбирать приращение где величина К градиентным методам примыкает метод [9], в к-ром приращение управления определяется из решения вспомогательной задачи линейного программирования. Большая группа прямых методов численного решения задач оптимального управления овнована на идеях последовательного анализа вариантов.,(см. [10], [11], [12]). Важным достоинством этих методов является то, что с их помощью удается решать задачи с фазовыми ограничениями вида
где С - замкнутое множество n-мерного пространства. Их основной недостаток - существенное возрастание трудностей с увеличением размерности пространства. Эти методы используют редукцию исходной задачи к задаче нелинейного программирования специального вида. Распространены два способа такой редукции. Согласно первому способу в конечном итоге получается задача минимизации функции, зависящей только от управлений, заданных в точках дискретной сетки на оси (см. [13]), Во втором способе (см. [12]) управление исключается и задача сводится к минимизации функции вида
где
к-рые получаются из ограничений (3), (4), (15). Для пояснения схемы решения задачи минимизации (16) при условиях (17) удобно использовать следующую геометрич. интерпретацию. Каждой совокупности векторов
На нулевом шаге определяется функция т. е. длина кратчайшего звена, соединяющего каждую точку x1 ОS1 с гиперплоскостью е 0. Так как то множество ломаных соединяющая каждую точку соединяющая каждую точку Формула (18) - рекуррентное соотношение, описывающее многошаговый процесс отыскания решения. На этом соотношении основаны динамич. программирование н принцип оптимальности Беллмана. В соответствии с (18) необходимо отыскивать минимум на множествах -длина отрезка, соединяющего два узла kи s всоседних гиперплоскостях, где минимум берется по номерам kвсех узлов, к-рые лежат в допустимой области Лит.:[1] Моисеев Н. Н., Численные методы в теории оптимальных систем, М., 1971; [2] Канторович Л. В., Крылов В. И., Приближенные методы высшего анализа, 5 изд., М.- Л., 1962: [3] Исаев В. К., Сонин В. В., "Ж. вычисл. матем. и матем. физ.", 1965, т. 5, № 2, с. 252-61; [4] Джурович С., Макинтайр Д., "Ракетная техника", 1962, JMS 9, с. 47-53; [5] Денхэм В., Брансон В., "Ракетная техника и космонавтика", 1964, № 1, с. 34-47; [6] Шатровский Л. И., "Ж. вычисл. матем. и матем. физ.", 1962, т. 2, № 3, с. 488-91; [7] Энеев Т. М., (.Космические исследования", 1966, т. 4, вып. 5, с. 651-69; [8] Крылов И. А., Черноусько Ф. Л., "Ж. вычисл. матем. и матем. физ.", 1962, т. 2, № 6, с. 1132-9; [9] Федоренко Р. П., там же, 1964, т. 4, № 6, с. 1045-64; [10] Беллиан Р., Динамическое программирование, пер. с англ., М., 1960; [11] Михалевич B.C., "Кибернетика", 1965, № 1, с. 45-46; [12J Моисеев Н. Н., там же, 1966, № 3. с. 1 - 29; [13] Ермольев Ю. М., Гуленко В. П., там же, 1967, № 3, С. 1-20. И. Б. Вапнярский, И. А. Ватель. |
|
|
|

 и управление
и управление  , доставляющие минимум функционалу
, доставляющие минимум функционалу 



 - векторы фазовых координат и управлений,
- векторы фазовых координат и управлений,  ,
,  - замкнутое множество m-мерного пространства, t - независимое переменное (время).
- замкнутое множество m-мерного пространства, t - независимое переменное (время). должно при каждом tдоставлять абсолютный максимум Гамильтона функции
должно при каждом tдоставлять абсолютный максимум Гамильтона функции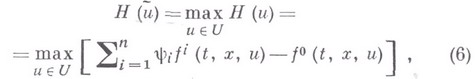
 определяется системой уравнений
определяется системой уравнений 
 и подставляется в (2) и (7). В результате получается замкнутая краевая задача для системы 2n дифференциальных уравнений (2) и (7) с 2n граничными условиями (3) и (4).
и подставляется в (2) и (7). В результате получается замкнутая краевая задача для системы 2n дифференциальных уравнений (2) и (7) с 2n граничными условиями (3) и (4).
 получается из решения задачи Коши для системы (2), (7) с начальными условиями (3) и
получается из решения задачи Коши для системы (2), (7) с начальными условиями (3) и  Невязки (8) рассматриваются как функции от неизвестных
Невязки (8) рассматриваются как функции от неизвестных  к-рые определяются из системы уравнений
к-рые определяются из системы уравнений

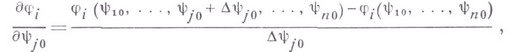
 получаются путем решения задачи Коши для системы (2), (7) с начальными условиями (3) и условпями
получаются путем решения задачи Коши для системы (2), (7) с начальными условиями (3) и условпями 
 - малое приращение величины
- малое приращение величины  .
. и, во-вторых, с неустойчивостью задачи Коши, к-рая особенно сильно проявляется на больших интервалах
и, во-вторых, с неустойчивостью задачи Коши, к-рая особенно сильно проявляется на больших интервалах  . Для преодоления первой трудности не существует универсального подхода. Для преодоления неустойчивости задачи Коши имеется ряд приемов (Коши задача;численные методы).
. Для преодоления первой трудности не существует универсального подхода. Для преодоления неустойчивости задачи Коши имеется ряд приемов (Коши задача;численные методы).


 - элементы бесконечной полной системы линейно независимых функций, удовлетворяющих граничным условиям
- элементы бесконечной полной системы линейно независимых функций, удовлетворяющих граничным условиям 

 , то а,- могут задаваться в виде
, то а,- могут задаваться в виде  ). Исходный функционал становится зависящим от Nфункций
). Исходный функционал становится зависящим от Nфункций  , к-рые могут определяться с помощью необходимых условий, т. е., в конечном счете, из решения краевой задачи для системы Nуравнений Эйлера.
, к-рые могут определяться с помощью необходимых условий, т. е., в конечном счете, из решения краевой задачи для системы Nуравнений Эйлера. вида
вида 

 производится следующим образом. С помощью уравнений в вариациях для (2) и сопряженной системы (7) с условиями на правом конце
производится следующим образом. С помощью уравнений в вариациях для (2) и сопряженной системы (7) с условиями на правом конце 
 представляется в виде
представляется в виде 
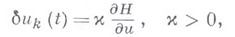
 вычисляется на управлении
вычисляется на управлении  и соответствующей ему траектории
и соответствующей ему траектории  . Законность линеаризации, а следовательно, и уменьшение функционала (13) обеспечиваются выбором достаточно малой величины
. Законность линеаризации, а следовательно, и уменьшение функционала (13) обеспечиваются выбором достаточно малой величины  . Процесс спуска (12) начинается с нек-рого
. Процесс спуска (12) начинается с нек-рого  и заканчивается, когда на нек-рой итерации
и заканчивается, когда на нек-рой итерации  становится меньше нек-рого заданного
становится меньше нек-рого заданного  Для описанного случая свободного правого конца алгоритм получается наиболее простым (см. [5], [6], [7]). Весьма эффективным для решения задач со свободным концом является метод (см. [8]), к-рый не использует линеаризации исходной задачи. В случае, когда граничные условия заданы и на правом конце, все эти алгоритмы существенно усложняются. Для учета граничных условий в [5] привлекается процедура проектирования градиента, а в [6] вводится штраф за невыполнение граничных условий, т. е. вместо (13) рассматривается функционал
Для описанного случая свободного правого конца алгоритм получается наиболее простым (см. [5], [6], [7]). Весьма эффективным для решения задач со свободным концом является метод (см. [8]), к-рый не использует линеаризации исходной задачи. В случае, когда граничные условия заданы и на правом конце, все эти алгоритмы существенно усложняются. Для учета граничных условий в [5] привлекается процедура проектирования градиента, а в [6] вводится штраф за невыполнение граничных условий, т. е. вместо (13) рассматривается функционал 


 - значение вектора хв точке
- значение вектора хв точке  при ограничениях
при ограничениях
 ставится в соответствие ломаная (см. рис.), к-рая проходит через точки
ставится в соответствие ломаная (см. рис.), к-рая проходит через точки  лежащие в гиперплоскостях
лежащие в гиперплоскостях  , задаваемых уравнениями
, задаваемых уравнениями  . Длина этой ломаной
. Длина этой ломаной  складывается из длин
складывается из длин  отдельных звеньев. Область допустимых значений
отдельных звеньев. Область допустимых значений  задается (17) и эта область отделяется от запретной нек-рой ломаной (на рис. запретная область заштрихована). Задача состоит в отыскании ломаной наименьшей длины, лежащей в допустимой области и соединяющей гиперплоскости
задается (17) и эта область отделяется от запретной нек-рой ломаной (на рис. запретная область заштрихована). Задача состоит в отыскании ломаной наименьшей длины, лежащей в допустимой области и соединяющей гиперплоскости  . Алгоритм решения задачи представляет собой многошаговый процесс, на каждом шаге iк-рого отметается нек-рое множество вариантов
. Алгоритм решения задачи представляет собой многошаговый процесс, на каждом шаге iк-рого отметается нек-рое множество вариантов  , заведомо не содержащее оптимальной ломаной.
, заведомо не содержащее оптимальной ломаной.
 .
.
 , не содержащих отрезка
, не содержащих отрезка  , может быть отброшено. На первом шаге строится кратчайшая ломаная
, может быть отброшено. На первом шаге строится кратчайшая ломаная 
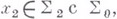 и множество ломаных
и множество ломаных  , не содержащих ломаной
, не содержащих ломаной  , также отбрасывается, и т. д. На i-м шаге строится кратчайшая ломаная
, также отбрасывается, и т. д. На i-м шаге строится кратчайшая ломаная 
 и отбрасывается множество ломаных
и отбрасывается множество ломаных  , не содержащих ломаной
, не содержащих ломаной  . На последнем шаге находится решение исходной задачи - кратчайшая ломаная, соединяющая гиперповерхности
. На последнем шаге находится решение исходной задачи - кратчайшая ломаная, соединяющая гиперповерхности  :
:
 , имеющих, вообще говоря, мощность континуума. При численной реализации используется их конечномерная аппроксимация. Для этого, кроме сетки, по t(напр., с постоянным шагом
, имеющих, вообще говоря, мощность континуума. При численной реализации используется их конечномерная аппроксимация. Для этого, кроме сетки, по t(напр., с постоянным шагом  ) строится сетка по
) строится сетка по  с шагом
с шагом  . Тогда задача сводится к отысканию кратчайшего пути на специальном графе с вершинами - узлами сетки. Пусть
. Тогда задача сводится к отысканию кратчайшего пути на специальном графе с вершинами - узлами сетки. Пусть  - узел
- узел  , лежащий в гиперплоскости
, лежащий в гиперплоскости  ;
;
 - длина наикратчайшего пути, соединяющего узел
- длина наикратчайшего пути, соединяющего узел  с гиперплоскостью
с гиперплоскостью  . Тогда рекуррентное соотношение (18) имеет вид
. Тогда рекуррентное соотношение (18) имеет вид 
 гиперплоскости
гиперплоскости  В общем случае этот минимум отыскивается перебором по всем узлам. Изложенный метод позволяет отыскивать глобальный экстремум функции (16) при ограничениях (3), (4), (15) с точностью, определяемой шагами сетки
В общем случае этот минимум отыскивается перебором по всем узлам. Изложенный метод позволяет отыскивать глобальный экстремум функции (16) при ограничениях (3), (4), (15) с точностью, определяемой шагами сетки  и
и  . Для сходимости метода к решению исходной задачи необходимо наличие определенных соотношений между этими шагами [напр., вида hj=о(t)]. Метод предъявляет большие требования к быстродействию и памяти ЭВМ. Поэтому при практич. реализации сначала находят экстремум на грубой сетке, а затем в окрестности полученного решения его уточняют на более мелкой сетке. Это делается с помощью одного из методов, позволяющих отыскивать локальный экстремум (см. Блуждающей трубки метод. Локальных вариаций метод, Бегущей волны метод).
. Для сходимости метода к решению исходной задачи необходимо наличие определенных соотношений между этими шагами [напр., вида hj=о(t)]. Метод предъявляет большие требования к быстродействию и памяти ЭВМ. Поэтому при практич. реализации сначала находят экстремум на грубой сетке, а затем в окрестности полученного решения его уточняют на более мелкой сетке. Это делается с помощью одного из методов, позволяющих отыскивать локальный экстремум (см. Блуждающей трубки метод. Локальных вариаций метод, Бегущей волны метод).