"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЭЙЛЕРА ПРЕОБРАЗОВАНИЕ
Значение ЭЙЛЕРА ПРЕОБРАЗОВАНИЕ в математической энциклопедии:
1) Э. п. рядов: если дан числовой ряд

то ряд

наа. рядом, полученным из ряда (1) Э. п. рядов. Здесь

Если ряд (1) сходится, то сходится и ряд (2) и притом к той же сумме, что и ряд (1). Если ряд (2) сходится (в этом случае ряд (1) может расходиться), то ряд (1) наз. суммируемым по Эйлеру.
Если ряд (1) сходится, an>0, для всех k=0,1, 2, ... последовательность

монотонная и

то сходимость ряда (2) быстрее сходимости ряда (1) (см. Сходимость).
Л. Д, Кудрявцев.
2) Э. п.- интегральное преобразование вида

где С - контур в комплексной плоскости с. Предложено Л. Эйлером (L. Euler, 1769).
Э. п, применяется к линейным обыкновенным дифференциальным уравнениям

где Qj(z) - многочлен степени  и
и  - константа. В таком виде можно представить любое линейное уравнение
- константа. В таком виде можно представить любое линейное уравнение

где Pj(z) - многочлены степени  степень Pn(z) равна n. Уравнение
степень Pn(z) равна n. Уравнение

наз. преобразованием Эйлера уравнения (2), Если w(z)определена формулой (1), причем  то справедливо тождество
то справедливо тождество

при условии, что внеинтегральная подстановка, к-рая возникает при интегрировании по частям, обращается в нуль. Отсюда видно, что если M(v)=0, то w(z) - решение уравнения (2).
Э. п. позволяет понизить порядок уравнения (2), если  при j>q, q<п. При q=0, q=1уравнение (2) интегрируется (см. Похгаммера уравнение).
при j>q, q<п. При q=0, q=1уравнение (2) интегрируется (см. Похгаммера уравнение).
Лит.:[1] Aйнс Э. Л., Обыкновенные дифференциальные уравнения, пер. с англ., Харьков, 1939; [2] Камке Э., Справочник по обыкновенным дифференциальным уравнениям, пер. г. нем., 5 изд., М., 1976.
М. В. Федорюк.
3) Э. п. - 1-го рода - интегральное преобразование вида

где 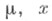 - комплексные переменные, причем путем интегрирования является отрезок
- комплексные переменные, причем путем интегрирования является отрезок 
Э. п. 1-го рода наз. также дробным интегралом Римана - Лиувилля порядка m. (Иногда под интегралом Римана - Лиувилля понимают интеграл

где а - комплексное число.)
При нек-рых условиях на функции f(x),g(x) имеют место следующие равенства:

 -комплексные постоянные,
-комплексные постоянные,

Э. п. 2-го рода - интегральное преобразование вида

где  - комплексные переменные, причем путем интегрирования является луч
- комплексные переменные, причем путем интегрирования является луч  или
или 
 При нек-рых условиях имеют место следующие равенства
При нек-рых условиях имеют место следующие равенства

 - комплексные постоянные,
- комплексные постоянные,

Э. п. 2-го рода иногда наз. дробным интегралом Bейля порядка 
Указанные преобразования введены также для обобщенных функций.
Лит.:Брычков Ю. А., Прудников А. П., Интегральные преобразования обобщенных функций, М., 1977.
Ю. А. Брычков, А. П. Прудников.








 и
и  - константа. В таком виде можно представить любое линейное уравнение
- константа. В таком виде можно представить любое линейное уравнение 
 степень Pn(z) равна n. Уравнение
степень Pn(z) равна n. Уравнение 
 то справедливо тождество
то справедливо тождество 
 при j>q, q<п. При q=0, q=1уравнение (2) интегрируется (см. Похгаммера уравнение).
при j>q, q<п. При q=0, q=1уравнение (2) интегрируется (см. Похгаммера уравнение). 
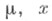 - комплексные переменные, причем путем интегрирования является отрезок
- комплексные переменные, причем путем интегрирования является отрезок 


 -комплексные постоянные,
-комплексные постоянные, 

 - комплексные переменные, причем путем интегрирования является луч
- комплексные переменные, причем путем интегрирования является луч  или
или 
 При нек-рых условиях имеют место следующие равенства
При нек-рых условиях имеют место следующие равенства 
 - комплексные постоянные,
- комплексные постоянные, 
