" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ШТИФЕЛЯ - УИТНИ КЛАСС

Значение ШТИФЕЛЯ - УИТНИ КЛАСС в математической энциклопедии:

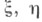характеристический класс со значениями в определенный для действительных векторных расслоений. Ш.- У. к. обозначаются через w_i, i>0, и для действительного векторного расслоения над топологич. пространством Вкласс лежит в введены Э. Штифелем [1] и X. Уитни [2]; они обладают следующими свойствами. 1) Для двух действительных векторных расслоений над общей базой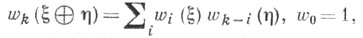

другими словами, где w= 1+w₁+ w₂ - полный Ш.- У. к. 2) Для одномерного универсального расслоения над имеет место равенство где y - ненулевой элемент группы Этими двумя свойствами Ш.- У. к. определяются однозначно. Ш.- У. к. стабильны, т. е. гдe - тривиальное расслоение и при Для ориентированного векторного расслоения размерности . над базой Вкласс совпадает с приведением по модулю 2 эйлерова класса.
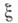Для векторного расслоения над . пусть - Тома пространство этого расслоения. Далее, пусть 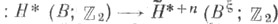-Тома изоморфизм. Тогда полный Ш. - У. к. совпадает с 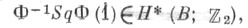где Sq=1+Sq¹+Sq²+. . . - полный Стинрода квадрат. Это свойство Ш.- У. к. можно использовать в качестве их определения. Ш.- У. к. гомотонически инвариантны в том смысле, что они совпадают для послойно-гомотопически эквивалентных расслоений над общей базой.
Любой характеристич. класс со значениями в определенный для действительных векторных расслоений, выражается через Ш.-У. <к.: кольца 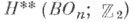и являются кольцами формальных степенных рядов от Ш.- У. к.:

Лит.:[1] Stiеfеl Е., лComm. math, helv.