"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ШТИФЕЛЯ МНОГООБРАЗИЕ
Значение ШТИФЕЛЯ МНОГООБРАЗИЕ в математической энциклопедии:
(вещественное) -многообразие Vn,k ортонормированных k-реперов в п-мерном евклидовом пространстве. Аналогично определяются комплексное Ш. м. Wn,k и кватернионное Ш. м. Wn,k. Ш. м. являются компактными вещественно-аналитич. многообразиями, а также однородными пространствами классич. компактных групп О(п), U(n)и Sp (п)соответственно. В частности, являются сферами, Ш. м. Vn,2 есть многообразие единичных касательных векторов к
являются сферами, Ш. м. Vn,2 есть многообразие единичных касательных векторов к  Ш. м. Vn,n, Wn,n, X п, п отождествляются с группами О(n), U(п),Sp (n), а Vn,n-1 - с группой S0(n). Рассматриваются также некомпактные Ш. м., состоящие из всевозможных k-реперов в
Ш. м. Vn,n, Wn,n, X п, п отождествляются с группами О(n), U(п),Sp (n), а Vn,n-1 - с группой S0(n). Рассматриваются также некомпактные Ш. м., состоящие из всевозможных k-реперов в 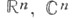 или
или 
Эти многообразия были введены Э. Штифелем [1] в связи с изучением систем линейно независимых векторных полей на гладких многообразиях. Начатое в |1] изучение топологии Ш. м. привело затем к полному вычислению их когомологий (см. [2], [3]). В частности,

 есть коммутативная алгебра с образующими xn-k, xn-k+1 , ..., xn-1 и соотношениями
есть коммутативная алгебра с образующими xn-k, xn-k+1 , ..., xn-1 и соотношениями
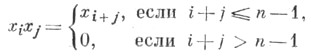
(через xl всюду обозначен элемент степени l). Вещественные, комплексные и кватернионные Ш. м. асферичны в размерностях не более п-k-1, 2( п-k) и 4(n-k)+2 соответственно, причем


По поводу вычисления других гомотопич. групп Ш. м. см. [5].
Лит.:[1] Stiefel E., лComm. math, helv.

 являются сферами, Ш. м. Vn,2 есть многообразие единичных касательных векторов к
являются сферами, Ш. м. Vn,2 есть многообразие единичных касательных векторов к  Ш. м. Vn,n, Wn,n, X п, п отождествляются с группами О(n), U(п),Sp (n), а Vn,n-1 - с группой S0(n). Рассматриваются также некомпактные Ш. м., состоящие из всевозможных k-реперов в
Ш. м. Vn,n, Wn,n, X п, п отождествляются с группами О(n), U(п),Sp (n), а Vn,n-1 - с группой S0(n). Рассматриваются также некомпактные Ш. м., состоящие из всевозможных k-реперов в 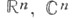 или
или 

 есть коммутативная алгебра с образующими xn-k, xn-k+1 , ..., xn-1 и соотношениями
есть коммутативная алгебра с образующими xn-k, xn-k+1 , ..., xn-1 и соотношениями