"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ШВАРЦА ФУНКЦИЯЗначение ШВАРЦА ФУНКЦИЯ в математической энциклопедии:
функция Римана - Шварца, - аналитич. ция, реализующая конформное отображение треугольника, ограниченного дугами окружностей, на верхнюю полуплоскость (или на единичный круг) и при неограниченном аналитич. родолжении остающаяся однозначной. Ш. ф. являются автоморфными функциями, группа к-рых зависит от вида отображаемого треугольника. Требованию однозначности можно удовлетворить лишь в том случае, если углы треугольника равны  где v1, v2, v3- нeк-рые специально подобранные натуральные числа. где v1, v2, v3- нeк-рые специально подобранные натуральные числа.
Если 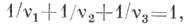 то получаются прямолинейные треугольники, для к-рых возможны только случаи: то получаются прямолинейные треугольники, для к-рых возможны только случаи: 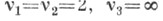 (полуполоса); v1=2, v2=3,v3=6; v1=2, v2=v3=4; v1=v2=v3=3. Во всех этих случаях Ш. ф. выражаются через тригонометрич. функции или через Вейерштрасса эллиптические функции и являются автоморфными функциями, группа к-рых есть группа движений евклидовой плоскости. Если 1/v1+1/v2+1/v3>1, то возможны следующие случаи: v1=v2=2, v3- любое; v1=2, v2=v3=3; v1=2, v2=3, v3=4; v1=2, v2=3, v3=5. Во всех этих случаях Ш. ф. являются рациональными автоморфными функциями, группа к-рых есть конечная группа движений сферы. Вследствие связи этой группы с правильными многогранниками такие Ш. <ф. наз. также полиэдральными функциями. (полуполоса); v1=2, v2=3,v3=6; v1=2, v2=v3=4; v1=v2=v3=3. Во всех этих случаях Ш. ф. выражаются через тригонометрич. функции или через Вейерштрасса эллиптические функции и являются автоморфными функциями, группа к-рых есть группа движений евклидовой плоскости. Если 1/v1+1/v2+1/v3>1, то возможны следующие случаи: v1=v2=2, v3- любое; v1=2, v2=v3=3; v1=2, v2=3, v3=4; v1=2, v2=3, v3=5. Во всех этих случаях Ш. ф. являются рациональными автоморфными функциями, группа к-рых есть конечная группа движений сферы. Вследствие связи этой группы с правильными многогранниками такие Ш. <ф. наз. также полиэдральными функциями.
Наконец, если 1/v1+1/v2+1/v3<1, то возможно бесконечно много различных треугольников, т. к. числа v1,v2,v3 можно неограниченно увеличивать. При этом Ш. ф. суть автоморфные функции с непрерывной особой линией (окружностью или прямой). В частности, случаи  и и  (круговой треугольник с нулевыми углами) приводят к модулярным функциям J(z) и (круговой треугольник с нулевыми углами) приводят к модулярным функциям J(z) и  соответственно. Ш. ф. изучались Г. Шварцем [1]. соответственно. Ш. ф. изучались Г. Шварцем [1]. Лит.:[1] Schwarz H., лJ. reine und angew. Math.
|

 где v1, v2, v3- нeк-рые специально подобранные натуральные числа.
где v1, v2, v3- нeк-рые специально подобранные натуральные числа. 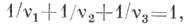 то получаются прямолинейные треугольники, для к-рых возможны только случаи:
то получаются прямолинейные треугольники, для к-рых возможны только случаи: 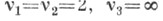 (полуполоса); v1=2, v2=3,v3=6; v1=2, v2=v3=4; v1=v2=v3=3. Во всех этих случаях Ш. ф. выражаются через тригонометрич. функции или через Вейерштрасса эллиптические функции и являются автоморфными функциями, группа к-рых есть группа движений евклидовой плоскости. Если 1/v1+1/v2+1/v3>1, то возможны следующие случаи: v1=v2=2, v3- любое; v1=2, v2=v3=3; v1=2, v2=3, v3=4; v1=2, v2=3, v3=5. Во всех этих случаях Ш. ф. являются рациональными автоморфными функциями, группа к-рых есть конечная группа движений сферы. Вследствие связи этой группы с правильными многогранниками такие Ш. <ф. наз. также полиэдральными функциями.
(полуполоса); v1=2, v2=3,v3=6; v1=2, v2=v3=4; v1=v2=v3=3. Во всех этих случаях Ш. ф. выражаются через тригонометрич. функции или через Вейерштрасса эллиптические функции и являются автоморфными функциями, группа к-рых есть группа движений евклидовой плоскости. Если 1/v1+1/v2+1/v3>1, то возможны следующие случаи: v1=v2=2, v3- любое; v1=2, v2=v3=3; v1=2, v2=3, v3=4; v1=2, v2=3, v3=5. Во всех этих случаях Ш. ф. являются рациональными автоморфными функциями, группа к-рых есть конечная группа движений сферы. Вследствие связи этой группы с правильными многогранниками такие Ш. <ф. наз. также полиэдральными функциями.  и
и  (круговой треугольник с нулевыми углами) приводят к модулярным функциям J(z) и
(круговой треугольник с нулевыми углами) приводят к модулярным функциям J(z) и  соответственно. Ш. ф. изучались Г. Шварцем [1].
соответственно. Ш. ф. изучались Г. Шварцем [1].