|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВАН ДЕР ПОЛЯ УРАВНЕНИЕЗначение ВАН ДЕР ПОЛЯ УРАВНЕНИЕ в математической энциклопедии: нелинейное обыкновенное дифференциальное уравнение 2-го порядка
Является важным частным случаем Лъенара уравнения. В. д. П. у. описывает свободные автоколебания одной из простейших нелинейных колебательных систем (осциллятора Ван дер Поля). В частности, уравнение (1) служит математич. моделью (при ряде упрощающих предположений) лампового генератора на триоде в случае кубич. характеристики лампы. Характер решений уравнения (1) был впервые подробно изучен Б. Ван дер Полем (см. [1]). Уравнение (1) эквивалентно системе двух уравнений относительно фазовых переменных Иногда вместо
являющемуся частным случаем Рэлея уравнения. Если вместе с переменной храссмотреть переменную ввести новое время При любом При малых m автоколебания осциллятора (1) близки к простым гармоническим колебаниям (см. Нелинейные колебания).с периодом 2p и с определенной амплитудой. Для вычисления колебательного процесса с большей точностью применяются асимптотич. методы. При возрастании m автоколебания осциллятора (1) все более отклоняются от гармонич. колебаний. При больших mуравнение (1) описывает релаксационные колебания с периодом (в первом приближении) Уравнение описывает поведение осциллятора Ван дер Поля под воздействием внешнего периодич. возмущения. Здесь наиболее важны изучение явления захватывания частоты (существования периодич. колебаний) и исследование биении (возможности почти периодич. колебаний; см. [2], [4]). . Лит.:[1] Vandеr Роl В., "Phil. Mag.", 1922, ser. 6, v. 43, p. 700-19; 1926, ser. 7, v. 2, p. 978-92; [2] Андронов А. А., Витт А. А., Xайкин С. Э., Теория колебаний, 2 изд., М., 1959; [3] Лефшец С., Геометрическая теория дифференциальных уравнений, пер. с англ., М., 1961; [41 Стокер Дж., Нелинейные колебания в механических и электрических системах, пер. с англ., 2 изд., М., 1953; [5] Дородницын А. А., "Прикл. матем. и механика", 1947, т. 11, с. 313-28; [6] Мищенко Е. Ф., Розов Н. X., Дифференциальные уравнения с малым параметром и релаксационные колебания, М., 1975. Н. X. Розов. |
|
|
|


 :
:
 удобнее ввести переменную
удобнее ввести переменную 
 тогда уравнение (1) приведется к уравнению
тогда уравнение (1) приведется к уравнению
 и положить
и положить  то
то  вместо уравнения (1) получим систему
вместо уравнения (1) получим систему  (3)
(3)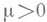 в фазовой плоскости системы (2) существует единственный устойчивый предельный цикл, к к-рому при
в фазовой плоскости системы (2) существует единственный устойчивый предельный цикл, к к-рому при  приближаются все остальные траектории (кроме положения равновесия в начале координат); этот предельный цикл адекватен автоколебаниям осциллятора Ван дер Поля (см. [2] - [4]).
приближаются все остальные траектории (кроме положения равновесия в начале координат); этот предельный цикл адекватен автоколебаниям осциллятора Ван дер Поля (см. [2] - [4]). . Известны более точные асимптотич. разложения величин, характеризующих релаксационные колебания (см. [5]); изучение этих колебаний равносильно исследованию решений системы (3) с малым параметром е при производной (см. [6]).
. Известны более точные асимптотич. разложения величин, характеризующих релаксационные колебания (см. [5]); изучение этих колебаний равносильно исследованию решений системы (3) с малым параметром е при производной (см. [6]).