"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧИСЕЛ ТЕОРИЯ
Значение ЧИСЕЛ ТЕОРИЯ в математической энциклопедии:
вероятностная - в широком смысле раздел теории чисел, в к-ром используются идеи и методы теории вероятностей.
Под вероятностной Ч. т. в узком смысле понимается статистич. теория распределения значений арифметических функций.
Подавляющее большинство арифметич. функций, изучаемых в теории чисел, являются аддитивными или мультипликативными, их значения обычно распределены очень сложно. Если проследить за изменением значении таких функций, когда аргумент пробегает последовательные натуральные числа, получится весьма хаотическая картина, к-рая обычно наблюдается при рассмотрении аддитивных свойств целых чисел совместно с мультипликативными. В классич. исследованиях при рассмотрении распределения значений действительных арифметич. функций f(m)обычно изучалось асимптотич. поведение самой функции f(т) или ее среднего значения. В первом случае ищутся простые функции  чтобы было
чтобы было  для всех тили хотя бы для всех достаточно больших т. Напр., если
для всех тили хотя бы для всех достаточно больших т. Напр., если  означает число всех различных простых делителей числа т, то
означает число всех различных простых делителей числа т, то  для всех т>1,
для всех т>1,  при
при 

Во втором случае рассматривается поведение

Для  среднее значение (1) равно (1+о(1) ln lnn). Решение как первой, так и второй задачи в общем случае дает мало информации о поведении функции f(m), об ее колебаниях. Функция может значительно отклоняться от своего среднего значения. При этом оказывается, что большие отклонения встречаются вообще довольно редко. Ставится задача отыскания границ, в к-рых могут колебаться значения функции f(m)для подавляющего большинства значении аргумента.
среднее значение (1) равно (1+о(1) ln lnn). Решение как первой, так и второй задачи в общем случае дает мало информации о поведении функции f(m), об ее колебаниях. Функция может значительно отклоняться от своего среднего значения. При этом оказывается, что большие отклонения встречаются вообще довольно редко. Ставится задача отыскания границ, в к-рых могут колебаться значения функции f(m)для подавляющего большинства значении аргумента.
Если f(m) - действительная аддитивная арифметич. функция,

где суммы берутся по простым числам . ипо степеням простых чисел  то
то

где с - абсолютная константа. Следовательно, для любого t>0 и всех  за исключением
за исключением  чисел, имеет место неравенство
чисел, имеет место неравенство

(аналог теоретико-вероятностного больших чисел закона). Для функции  это неравенство можно записать в виде
это неравенство можно записать в виде

Пусть через Nn(. . .) обозначено число натуральных 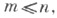 удовлетворяющих условиям, к-рые будут указываться в скобках вместо многоточия. Желая более точно охарактеризовать распределение значении действительных арифметич. функций f(т), приходят к рассмотрению асимптотич. поведения частоты
удовлетворяющих условиям, к-рые будут указываться в скобках вместо многоточия. Желая более точно охарактеризовать распределение значении действительных арифметич. функций f(т), приходят к рассмотрению асимптотич. поведения частоты

при  где Е - любое борелевское множество. Среди асимптотич. законов для (3) наибольший интерес представляют законы двух типов: интегральные и локальные.
где Е - любое борелевское множество. Среди асимптотич. законов для (3) наибольший интерес представляют законы двух типов: интегральные и локальные.
Интегральные законы. Изучается асимптотич. поведение функции распределения
 при
при  и ладанных С п, Dn.
и ладанных С п, Dn.
В случае арифметических аддитивных функции ищутся условия, при к-рых Fn(Cn+Dnx) стремится к нек-рой функции распределения F(х)во всех ее точках непрерывности. При этом, если F(х)нe вырождены, то Dn обязательно должно стремиться к конeчному (отличному от 0) или бесконечному пределу.
В случае конечного предела достаточно ограничиться рассмотрением Fn(Cn+x). Для того чтобы Fn(Cn+x) с какими-либо С n при  имела невырожденное предельное распределение, необходимо и достаточно, чтобы f(т) имела вид
имела невырожденное предельное распределение, необходимо и достаточно, чтобы f(т) имела вид  где а - константа, а функция g(m)удовлетворяет условиям
где а - константа, а функция g(m)удовлетворяет условиям

При этом С n должны быть равными

С - константа. Выбор С п однозначен с точностью до слагаемых C+o(l). Предельное распределение является дискретным, когда  и непрерывным в противном случае.
и непрерывным в противном случае.
В частности, Fn(x)(случай С n=0) тогда и только тогда имеет предельное распределение, когда сходятся ряды

(аналог теоретико-вероятностной теоремы о трех рядах).
Случай  не исследован до конца. Ниже приведены нек-рые наиболее простые результаты, когда С п=А п и Dn= Bn определены формулами (2).
не исследован до конца. Ниже приведены нек-рые наиболее простые результаты, когда С п=А п и Dn= Bn определены формулами (2).
Если для всякого фиксированного 

при  (аналог условия Линдеберга, см. Линдеберга - Феллера теорема), то
(аналог условия Линдеберга, см. Линдеберга - Феллера теорема), то

(нормальный закон). Если выполнено (4), то В п является медленно меняющейся функцией от ln. в смысле Карамата. Более того, если Bn является такой функцией, то для справедливости (5) условие (4) является необходимым.
Пусть Bn является медленно меняющейся функцией от ln п. Для того чтобы Fn( А п+ В п х )сходилась к предельному распределению с дисперсией 1, необходимо и достаточно, чтобы существовала такая неубывающая функция 
что при  для всех и, за исключением, быть может, u=0,
для всех и, за исключением, быть может, u=0,

Характеристич. функция j(t) предельного закона в случае его существования определяется формулой

Изучается быстрота сходимости к предельному закону. Так, напр., если f(т)- сильно аддитивная функция и

при  то
то  равномерно по x.
равномерно по x.
Для мультипликативных арифметич. функций имеют место аналогичные результаты.
Локальные законы. Изучается поведение при  частоты
частоты  при заданных с. В случае действительных аддитивных арифметич. функций эта частота всегда имеет предел, к-рый отличен от 0 лишь для не более чем счетного множества значений с. Пусть
при заданных с. В случае действительных аддитивных арифметич. функций эта частота всегда имеет предел, к-рый отличен от 0 лишь для не более чем счетного множества значений с. Пусть

- не равные нулю пределы, причем хотя бы один такой предел существует. Тогда

и
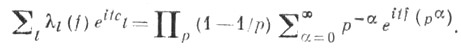
Если f(т) принимает лишь целые значения,
 то
то  тогда и только тогда, когда
тогда и только тогда, когда 
Изучается скорость сходимости к  Существует такая абсолютная константа С, что для всех целых kи всех целозначных аддитивных арифметич. функций f(т) с условием f(р)=0 для всех простых р
Существует такая абсолютная константа С, что для всех целых kи всех целозначных аддитивных арифметич. функций f(т) с условием f(р)=0 для всех простых р

Изучается также асимптотич. поведение частоты  когда kn может расти вместе с п.
когда kn может расти вместе с п.
Лит.:[1] Кац М., Статистическая независимость в теории вероятностей, анализе и теории чисел, пер. с англ., М., 1963; [2] Кубилюс Й. П., Вероятностные методы в теории чисел, 2 изд., Вильнюс, 1962; [3] его же, в сб.: Актуальные проблемы аналитической теории чисел, Минск, 1974; [4] Линник Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [5] eго же, Эргодические свойства алгебраических полей, Л., 1967; [6] Постников А. Г., Эргодические вопросы теории сравнений и теории диофантовых приближений, М., 1966; [7] Elliоtt P. D. T. A., Probabilistic number theory, v. 1-2, N.-Y.- Hdlb.- В., 1979-80.
Я. П. Кубилюс.

 чтобы было
чтобы было  для всех тили хотя бы для всех достаточно больших т. Напр., если
для всех тили хотя бы для всех достаточно больших т. Напр., если  означает число всех различных простых делителей числа т, то
означает число всех различных простых делителей числа т, то  для всех т>1,
для всех т>1,  при
при 


 среднее значение (1) равно (1+о(1) ln lnn). Решение как первой, так и второй задачи в общем случае дает мало информации о поведении функции f(m), об ее колебаниях. Функция может значительно отклоняться от своего среднего значения. При этом оказывается, что большие отклонения встречаются вообще довольно редко. Ставится задача отыскания границ, в к-рых могут колебаться значения функции f(m)для подавляющего большинства значении аргумента.
среднее значение (1) равно (1+о(1) ln lnn). Решение как первой, так и второй задачи в общем случае дает мало информации о поведении функции f(m), об ее колебаниях. Функция может значительно отклоняться от своего среднего значения. При этом оказывается, что большие отклонения встречаются вообще довольно редко. Ставится задача отыскания границ, в к-рых могут колебаться значения функции f(m)для подавляющего большинства значении аргумента. 
 то
то 
 за исключением
за исключением  чисел, имеет место неравенство
чисел, имеет место неравенство 
 это неравенство можно записать в виде
это неравенство можно записать в виде 
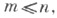 удовлетворяющих условиям, к-рые будут указываться в скобках вместо многоточия. Желая более точно охарактеризовать распределение значении действительных арифметич. функций f(т), приходят к рассмотрению асимптотич. поведения частоты
удовлетворяющих условиям, к-рые будут указываться в скобках вместо многоточия. Желая более точно охарактеризовать распределение значении действительных арифметич. функций f(т), приходят к рассмотрению асимптотич. поведения частоты 
 где Е - любое борелевское множество. Среди асимптотич. законов для (3) наибольший интерес представляют законы двух типов: интегральные и локальные.
где Е - любое борелевское множество. Среди асимптотич. законов для (3) наибольший интерес представляют законы двух типов: интегральные и локальные.  при
при  и ладанных С п, Dn.
и ладанных С п, Dn.  имела невырожденное предельное распределение, необходимо и достаточно, чтобы f(т) имела вид
имела невырожденное предельное распределение, необходимо и достаточно, чтобы f(т) имела вид  где а - константа, а функция g(m)удовлетворяет условиям
где а - константа, а функция g(m)удовлетворяет условиям 

 и непрерывным в противном случае.
и непрерывным в противном случае. 
 не исследован до конца. Ниже приведены нек-рые наиболее простые результаты, когда С п=А п и Dn= Bn определены формулами (2).
не исследован до конца. Ниже приведены нек-рые наиболее простые результаты, когда С п=А п и Dn= Bn определены формулами (2). 

 (аналог условия Линдеберга, см. Линдеберга - Феллера теорема), то
(аналог условия Линдеберга, см. Линдеберга - Феллера теорема), то 

 для всех и, за исключением, быть может, u=0,
для всех и, за исключением, быть может, u=0, 


 то
то  равномерно по x.
равномерно по x.  частоты
частоты  при заданных с. В случае действительных аддитивных арифметич. функций эта частота всегда имеет предел, к-рый отличен от 0 лишь для не более чем счетного множества значений с. Пусть
при заданных с. В случае действительных аддитивных арифметич. функций эта частота всегда имеет предел, к-рый отличен от 0 лишь для не более чем счетного множества значений с. Пусть 

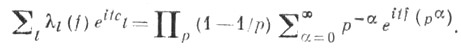
 то
то  тогда и только тогда, когда
тогда и только тогда, когда 
 Существует такая абсолютная константа С, что для всех целых kи всех целозначных аддитивных арифметич. функций f(т) с условием f(р)=0 для всех простых р
Существует такая абсолютная константа С, что для всех целых kи всех целозначных аддитивных арифметич. функций f(т) с условием f(р)=0 для всех простых р 
 когда kn может расти вместе с п.
когда kn может расти вместе с п.