"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕТАЕВА УРАВНЕНИЯ
Значение ЧЕТАЕВА УРАВНЕНИЯ в математической энциклопедии:
- общие канонич. уравнения механики голономных систем, представимые с помощью нек-рой группы Ли бесконечно малых преобразований и эквивалентные Пуанкаре уравнениям.
Если вместо независимых переменных  определяющих действительные перемещения, ввести величины
определяющих действительные перемещения, ввести величины

 - функция Лагранжа, то уравнения Пуанкаре примут более простой вид Ч. у.
- функция Лагранжа, то уравнения Пуанкаре примут более простой вид Ч. у.
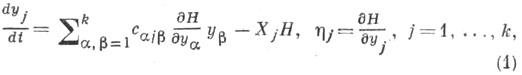
где

-функция Гамильтона. Вторую группу уравнений (1) можно заменить уравнениями
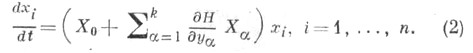
Вводя функцию действия по формуле
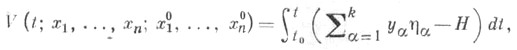
где интегрирование происходит по действительной траектории системы, можно получить соотношения

Здесь 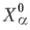 обозначают операторы
обозначают операторы 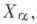 отнесенные к начальному моменту времени t0 и начальному положению системы
отнесенные к начальному моменту времени t0 и начальному положению системы  - начальные значения
- начальные значения  Если функция действия известна, то уравнения (3) решают задачу механики, причем вторая группа уравнений (3) определяет в неявном виде закон движения системы. Функция действия удовлетворяет дифференциальному уравнению с частными производными 1-го порядка
Если функция действия известна, то уравнения (3) решают задачу механики, причем вторая группа уравнений (3) определяет в неявном виде закон движения системы. Функция действия удовлетворяет дифференциальному уравнению с частными производными 1-го порядка

Если известен полный интеграл V(t, x1, ..., х п, a1, ... ..., an) уравнения (4), то решения Ч. у. определяются соотношениями
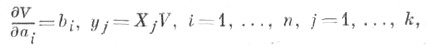
где ai, bi - произвольные постоянные, стесненные п-k проинтегрированными уравнениями связей.
Вместо переменных xi могут быть рассмотрены новые переменные  определяющие положение системы. Пусть
определяющие положение системы. Пусть  As , s = 1, ..., kпредставляют (k+ 1)-членную группу непрерывных преобразований Ли в переменных
As , s = 1, ..., kпредставляют (k+ 1)-членную группу непрерывных преобразований Ли в переменных  со структурными постоянными
со структурными постоянными  причем
причем  и
и  -переменные, определяющие возможные и действительные перемещения, так что для нек-рой функции
-переменные, определяющие возможные и действительные перемещения, так что для нек-рой функции
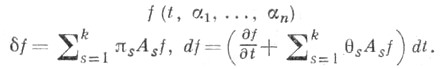
Преобразование переменных определяется характеристич. функцией

и формулами

вместе с проинтегрированными уравнениями связей. Такие преобразования наз. канонич. преобразованиями, они сохраняют канонич. вид уравнений движения, причем функция Гамильтона в новых переменных принимает вид
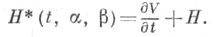
Если характеристич. функция преобразования является полным интегралом уравнения (4) ( при 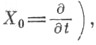 то функция H* = 0 и Ч. у. (1), (2) в новых переменных принимают вид
то функция H* = 0 и Ч. у. (1), (2) в новых переменных принимают вид

т. е. 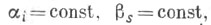 .= l, ..., п, s = l,..., k. Линейная форма
.= l, ..., п, s = l,..., k. Линейная форма  определяет основной относительный интегральный инвариант динамики.
определяет основной относительный интегральный инвариант динамики.
Условие того, что f(t, x1, ..., х п, y1, ..., yk)=const, есть первый интеграл Ч. у., имеет вид  где
где

- скобка Пуассона.
Если f=а и g=b являются первыми интегралами, то интегралом будет и (f, g)=с (обобщение Пуассона теоремы).
Ч. у. выведены H. Г. Четаевым [1]-[3], разработавшим и их теорию.
Лит.:[1] Четаeв H. Г., лС. r. Acad. sci.

 определяющих действительные перемещения, ввести величины
определяющих действительные перемещения, ввести величины 
 - функция Лагранжа, то уравнения Пуанкаре примут более простой вид Ч. у.
- функция Лагранжа, то уравнения Пуанкаре примут более простой вид Ч. у. 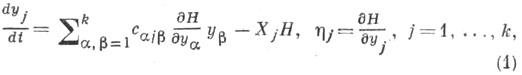

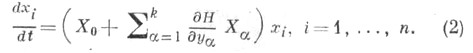
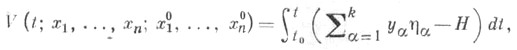

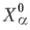 обозначают операторы
обозначают операторы 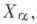 отнесенные к начальному моменту времени t0 и начальному положению системы
отнесенные к начальному моменту времени t0 и начальному положению системы  - начальные значения
- начальные значения  Если функция действия известна, то уравнения (3) решают задачу механики, причем вторая группа уравнений (3) определяет в неявном виде закон движения системы. Функция действия удовлетворяет дифференциальному уравнению с частными производными 1-го порядка
Если функция действия известна, то уравнения (3) решают задачу механики, причем вторая группа уравнений (3) определяет в неявном виде закон движения системы. Функция действия удовлетворяет дифференциальному уравнению с частными производными 1-го порядка 
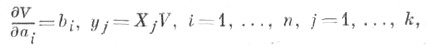
 определяющие положение системы. Пусть
определяющие положение системы. Пусть  As , s = 1, ..., kпредставляют (k+ 1)-членную группу непрерывных преобразований Ли в переменных
As , s = 1, ..., kпредставляют (k+ 1)-членную группу непрерывных преобразований Ли в переменных  со структурными постоянными
со структурными постоянными  причем
причем  и
и  -переменные, определяющие возможные и действительные перемещения, так что для нек-рой функции
-переменные, определяющие возможные и действительные перемещения, так что для нек-рой функции 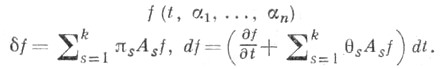


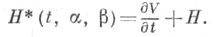
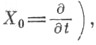 то функция H* = 0 и Ч. у. (1), (2) в новых переменных принимают вид
то функция H* = 0 и Ч. у. (1), (2) в новых переменных принимают вид 
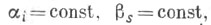 .= l, ..., п, s = l,..., k. Линейная форма
.= l, ..., п, s = l,..., k. Линейная форма  определяет основной относительный интегральный инвариант динамики.
определяет основной относительный интегральный инвариант динамики.  где
где 