"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕТАЕВА ТЕОРЕМЫ
Значение ЧЕТАЕВА ТЕОРЕМЫ в математической энциклопедии:
1) Ч. т. о неустойчивости - общие теоремы о неустойчивости движения, установленные Н. Г. Четаевым для уравнений возмущенного движения вида

правые части к-рых Xs - голоморфные функции относительно действительных переменных xs с коэффициентами, являющимися непрерывными и ограниченными функциями действительной переменной - времени t, определенные в нек-рой области

причем Xs(t,0, ... , 0) = 0.
Ч. т. даны в двух формулировках: с двумя функциями V, W и с одной функцией V. Под функциями V, . понимаются действительные функции действительных переменных xs и t, однозначные и непрерывные в области (2) и обращающиеся в нуль при xs=0, так же как их полные производные по времени 1-го порядка V, W, причем, напр.,

Теорема о неустойчивости с двумя функциями (1934, см. [1], с. 222-24): если дифференциальные уравнения таковы, что: 1) для нек-рой допускающей бесконечно малый высший предел функции . существует область, где  и 2) для нек-рых значений величин xs, численно сколь угодно малых, в области
и 2) для нек-рых значений величин xs, численно сколь угодно малых, в области  возможно выделить область, в к-рой нек-рая функция W>0, на границе области W=0значения
возможно выделить область, в к-рой нек-рая функция W>0, на границе области W=0значения  суть одного какого-либо определенного знака, то невозмущенное движение х=0 неустойчиво.
суть одного какого-либо определенного знака, то невозмущенное движение х=0 неустойчиво.
При решении вопроса о неустойчивости целесообразно рассматривать интервал изменения времени  закрытым и существование области V>0 понимать как ее непустоту для любого tна этом интервале (см. [1], с. 225-238). Если рассматриваемая область
закрытым и существование области V>0 понимать как ее непустоту для любого tна этом интервале (см. [1], с. 225-238). Если рассматриваемая область  ограничена V=0 и при этом
ограничена V=0 и при этом  то за функцию Wвозможно взять функцию V.
то за функцию Wвозможно взять функцию V.
Условие 2) можно сформулировать многими иными способами, в частности, пусть уравнения (1) имеют первый интеграл F(t, x)=const,обладающий свойствами функций V, и пусть область F>0 не является пустой при численно сколь угодно малых значениях xs (см. [1], с. 232). Если для возмущенных движений при  сколь бы мало е не было, тем самым будут выполняться неравенства
сколь бы мало е не было, тем самым будут выполняться неравенства  в области (2) для допускающей малый высший предел функции V, а начальные значения xs0 при удовлетворении интегралу
в области (2) для допускающей малый высший предел функции V, а начальные значения xs0 при удовлетворении интегралу  возможно выбрать так, чтобы они удовлетворяли также н неравенству V0>0, то невозмущенное движение неустойчиво.
возможно выбрать так, чтобы они удовлетворяли также н неравенству V0>0, то невозмущенное движение неустойчиво.
Если интервал времени считать открытым  и не вводить условного смысла существования области V>0, то справедлива теорема о неустойчивости с одной функцией (1946, см. [1], с. 5-152): если дифференциальные уравнения (1) таковы, что возможно найти функцию V, ограниченную в области V>0, существующей при всяком
и не вводить условного смысла существования области V>0, то справедлива теорема о неустойчивости с одной функцией (1946, см. [1], с. 5-152): если дифференциальные уравнения (1) таковы, что возможно найти функцию V, ограниченную в области V>0, существующей при всяком 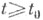 и для сколь угодно малых по абсолютной величине значений переменных xs, производная к-рой
и для сколь угодно малых по абсолютной величине значений переменных xs, производная к-рой  была бы определенно-положительной в области. V>0, то невозмущенное движение неустойчиво. Под определенно положительной в области V>0 функцией понимается функция W(t, x), к-рая может обращаться в нуль в этой области лишь на границе V=0, причем для произвольного
была бы определенно-положительной в области. V>0, то невозмущенное движение неустойчиво. Под определенно положительной в области V>0 функцией понимается функция W(t, x), к-рая может обращаться в нуль в этой области лишь на границе V=0, причем для произвольного  как бы мало оно не было выбрано, найдется такое число l>0, что при xs, удовлетворяющих условию
как бы мало оно не было выбрано, найдется такое число l>0, что при xs, удовлетворяющих условию  и для всякого
и для всякого  имеет место неравенство
имеет место неравенство 
Было дaно обращение этой теоремы, чем была обоснована ее универсальность (см. [2]).
2) Ч. т.- теорема о свойствах уравнений в вариациях Пуанкаре

составленных для невозмущенного движения qi=qi(t), pi=pi(t). предполагаемого таким, что коэффициенты уравнений (3) суть непрерывные ограниченные действительные функции t, Н(t, qi, pi) - функция Гамильтона,  и
и  -отклонения координат qi и импульсов р i. Уравнения (3) имеют существенное значение в исследованиях устойчивости движений консервативных голонимных систем.
-отклонения координат qi и импульсов р i. Уравнения (3) имеют существенное значение в исследованиях устойчивости движений консервативных голонимных систем.
Теорема. Если невозмущенное движение голономной потенциальной системы устойчиво, то характеристич. числа всех решений уравнений в вариациях (3) равны нулю, уравнения (3) являются при этом правильными и приводимыми к системе уравнений с постоянными коэффициентами и имеют знакоопределенный квадратичный интеграл.
Ч. т. обобщает теорему Лагранжа для равновесий и теорему Пуанкаре - Ляпунова для периодич. движений. Согласно теореме, для устойчивого невозмущенного движения потенциальной системы бесконечно близкие возмущенные движения имеют колебательный, волновой характер. Отсюда Н. Г. Четаев сделал вывод, что если существует аналогия между динамикой и математич. теорией света Коши, то ее следует искать в возмущенных движениях вблизи устойчивых движений потенциальных систем. И такую аналогию H. Г. Четаев нашел (см. [1], с. 404-06), показав, что необходимое условие устойчивости голономных консервативных систем приводит к волновому уравнению. Оптико-механическая аналогия полно исследована Н. Г. Четаевым и в свете теории групп Ли, причем в основу положена оригинальная мысль о существе аналогии между двумя явлениями как о совпадении группы преобразований одного явления (колебательного процесса распространения света) с группой преобразований другого явления (возмущенных движений консервативной системы вблизи ее устойчивого движения). Н. Г. Четаев доказал (см. [1], с.393-403), что эта последняя группа представляет собой унимодулярную группу линейных преобразований, имеющую представление в полной группе преобразований Лоренца - основной для теории света Коши Максвелла.
Лит.:[1] Четаев Н. Г., Устойчивость движения. Работы по аналитической механике, М., 1962; [2] Красавский Н. Н., Некоторые задачи теории устойчивости движения, М., 1951).
В. В. Румянцев.




 и 2) для нек-рых значений величин xs, численно сколь угодно малых, в области
и 2) для нек-рых значений величин xs, численно сколь угодно малых, в области  возможно выделить область, в к-рой нек-рая функция W>0, на границе области W=0значения
возможно выделить область, в к-рой нек-рая функция W>0, на границе области W=0значения  суть одного какого-либо определенного знака, то невозмущенное движение х=0 неустойчиво.
суть одного какого-либо определенного знака, то невозмущенное движение х=0 неустойчиво.  закрытым и существование области V>0 понимать как ее непустоту для любого tна этом интервале (см. [1], с. 225-238). Если рассматриваемая область
закрытым и существование области V>0 понимать как ее непустоту для любого tна этом интервале (см. [1], с. 225-238). Если рассматриваемая область  ограничена V=0 и при этом
ограничена V=0 и при этом  то за функцию Wвозможно взять функцию V.
то за функцию Wвозможно взять функцию V.  сколь бы мало е не было, тем самым будут выполняться неравенства
сколь бы мало е не было, тем самым будут выполняться неравенства  в области (2) для допускающей малый высший предел функции V, а начальные значения xs0 при удовлетворении интегралу
в области (2) для допускающей малый высший предел функции V, а начальные значения xs0 при удовлетворении интегралу  возможно выбрать так, чтобы они удовлетворяли также н неравенству V0>0, то невозмущенное движение неустойчиво.
возможно выбрать так, чтобы они удовлетворяли также н неравенству V0>0, то невозмущенное движение неустойчиво.  и не вводить условного смысла существования области V>0, то справедлива теорема о неустойчивости с одной функцией (1946, см. [1], с. 5-152): если дифференциальные уравнения (1) таковы, что возможно найти функцию V, ограниченную в области V>0, существующей при всяком
и не вводить условного смысла существования области V>0, то справедлива теорема о неустойчивости с одной функцией (1946, см. [1], с. 5-152): если дифференциальные уравнения (1) таковы, что возможно найти функцию V, ограниченную в области V>0, существующей при всяком 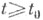 и для сколь угодно малых по абсолютной величине значений переменных xs, производная к-рой
и для сколь угодно малых по абсолютной величине значений переменных xs, производная к-рой  была бы определенно-положительной в области. V>0, то невозмущенное движение неустойчиво. Под определенно положительной в области V>0 функцией понимается функция W(t, x), к-рая может обращаться в нуль в этой области лишь на границе V=0, причем для произвольного
была бы определенно-положительной в области. V>0, то невозмущенное движение неустойчиво. Под определенно положительной в области V>0 функцией понимается функция W(t, x), к-рая может обращаться в нуль в этой области лишь на границе V=0, причем для произвольного  как бы мало оно не было выбрано, найдется такое число l>0, что при xs, удовлетворяющих условию
как бы мало оно не было выбрано, найдется такое число l>0, что при xs, удовлетворяющих условию  и для всякого
и для всякого  имеет место неравенство
имеет место неравенство 

 и
и  -отклонения координат qi и импульсов р i. Уравнения (3) имеют существенное значение в исследованиях устойчивости движений консервативных голонимных систем.
-отклонения координат qi и импульсов р i. Уравнения (3) имеют существенное значение в исследованиях устойчивости движений консервативных голонимных систем.