"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕПМЕНА - ЭНСКОГА МЕТОД
Значение ЧЕПМЕНА - ЭНСКОГА МЕТОД в математической энциклопедии:
способ получения решения Болъцмана уравнения (кинетического) для одночастичной функции распределения f (t, r, v), являющийся своеобразным методом последовательных приближений, в к-ром локальное распределение Максвелла  определяется стандартной формулой, но с локальными значениями плотности числа частиц n(t, r), гидродинамич. скорости и(t, r )и температуры
определяется стандартной формулой, но с локальными значениями плотности числа частиц n(t, r), гидродинамич. скорости и(t, r )и температуры  используется в качестве нулевого приближения, а условием существования решения для следующих приближений является выполнение гидродинамич. уравнений для n, и,
используется в качестве нулевого приближения, а условием существования решения для следующих приближений является выполнение гидродинамич. уравнений для n, и,  в предыдущем приближении. Так как свертки по скорости vинтеграла столкновений Больцмана с величинами 1, v и v2 равны нулю, то в эти уравнения движения для п, и п
в предыдущем приближении. Так как свертки по скорости vинтеграла столкновений Больцмана с величинами 1, v и v2 равны нулю, то в эти уравнения движения для п, и п  интеграл столкновений явно не входит. Решение самого уравнения Больцмана ищется в виде
интеграл столкновений явно не входит. Решение самого уравнения Больцмана ищется в виде

что приводит к неоднородному интегральному уравнению с линеаризованным относительно функции  интегралом столкновений. Неоднородная часть уравнения содержит величины n(t,r), u(t,r),
интегралом столкновений. Неоднородная часть уравнения содержит величины n(t,r), u(t,r), 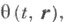 подчиненные упомянутым выше уравнениям. Таким образом, совместно рассматриваются сразу шесть уравнений. Решение уравнения для
подчиненные упомянутым выше уравнениям. Таким образом, совместно рассматриваются сразу шесть уравнений. Решение уравнения для  ищется в виде разложения по многочленам Сонина (присоединенные многочлены Лагерра полуцелого индекса) в пространстве скоростей. Для всего метода характерно, что зависимость функции распределения f(t, r, v) от времени входит только через ее зависимость от локальных величин n(t, r), u(t, r),
ищется в виде разложения по многочленам Сонина (присоединенные многочлены Лагерра полуцелого индекса) в пространстве скоростей. Для всего метода характерно, что зависимость функции распределения f(t, r, v) от времени входит только через ее зависимость от локальных величин n(t, r), u(t, r),  Нулевое приближение f=f лок определяет уравнения гидродинамики идеальной жидкости (уравнения Эйлера), к-рые являются условием существования первого приближения для f, ему же соответствуют уже уравнения Навье-Стокса с явными выражениями для коэффициентов диффузии, теплопроводности и двух вязкостен, следующий шаг - уравнение Бэрнетта и т. д. Параметром разложения является, по существу, относительное изменение величин n(t, r), u(t, r),
Нулевое приближение f=f лок определяет уравнения гидродинамики идеальной жидкости (уравнения Эйлера), к-рые являются условием существования первого приближения для f, ему же соответствуют уже уравнения Навье-Стокса с явными выражениями для коэффициентов диффузии, теплопроводности и двух вязкостен, следующий шаг - уравнение Бэрнетта и т. д. Параметром разложения является, по существу, относительное изменение величин n(t, r), u(t, r), на интервале, равном средней длине свободного пробега (параметр неоднородности), поэтому для задач со скачками этих величин (ударные волны и т. п.) метод не может быть использован.
на интервале, равном средней длине свободного пробега (параметр неоднородности), поэтому для задач со скачками этих величин (ударные волны и т. п.) метод не может быть использован.
Изложенный метод решения, основанный на идее решения интегральных уравнений Д. Гильберта (D. Hilbert, 1912), был разработан Д. Энскогом (D. Enskog, 1917) и независимо С. Чепменом (S. Chapman, 1916).
То же решение можно получить методом Греда [5], не столь громоздким, как Ч.- Э. м. При этом функция f представляется в виде ряда по производным  по компонентам скорости V(что фактически эквивалентно разложению функции по многочленам Эрмита в трехмерном пространстве скоростей) с зависящими от tи rкоэффициентами, являющимися моментами искомой функции распределения, к-рые и определяются с помощью уравнения Больцмана. Первое приближение для f (приводящее к уравнениям Навье- Стокса) содержит только вторые производные от f лок.
по компонентам скорости V(что фактически эквивалентно разложению функции по многочленам Эрмита в трехмерном пространстве скоростей) с зависящими от tи rкоэффициентами, являющимися моментами искомой функции распределения, к-рые и определяются с помощью уравнения Больцмана. Первое приближение для f (приводящее к уравнениям Навье- Стокса) содержит только вторые производные от f лок.
Полученное указанными методами решение для одночастичной функции распределения можно вывести непосредственно из Боголюбова цепочки уравнений в соответствующем малому значению параметра неоднородности гидродинамическом приближении (т. е. минуя кинетич. уравнение). Однако т. к. последовательные приближения, производимые в цепочке, будут включать учет корреляций более высокого порядка, то совпадение результатов произойдет лишь до первого порядка включительно, т. к. следующее приближение для f уже учитывает тронные корреляции частиц, к-рых уравнение Больцмана не содержит, причем вклады от этих членов конкурируют с теми членами, к-рые соответствуют второму приближению для функции f, удовлетворяющей стандартному уравнению Больцмана.
Лит.:[1] Чепмен С., Каулинг Т. Д., Математическая теория неоднородных газов, пер. с англ., М., 1960; [2] Уленбек Дж., Форд Дж.. Лекции по статистической механике, пер. с англ., М., 1965; [3] Гиршфельдер Д ж., Кертис Ч., Берд Р., Молекулярная теория газов и жидкостей, пер. с англ., М., 1961; [4] Грэд Г., в кн.: Некоторые вопросы кинетической теории газов, пер. с англ., М., 1965, с. 7-128; [5] Grаd H., в кн.: Handbuch der Physik, Bd 12, В.- [а. о.], 1958, S. 205 -94.
И. А. Квасников.

 определяется стандартной формулой, но с локальными значениями плотности числа частиц n(t, r), гидродинамич. скорости и(t, r )и температуры
определяется стандартной формулой, но с локальными значениями плотности числа частиц n(t, r), гидродинамич. скорости и(t, r )и температуры  используется в качестве нулевого приближения, а условием существования решения для следующих приближений является выполнение гидродинамич. уравнений для n, и,
используется в качестве нулевого приближения, а условием существования решения для следующих приближений является выполнение гидродинамич. уравнений для n, и,  в предыдущем приближении. Так как свертки по скорости vинтеграла столкновений Больцмана с величинами 1, v и v2 равны нулю, то в эти уравнения движения для п, и п
в предыдущем приближении. Так как свертки по скорости vинтеграла столкновений Больцмана с величинами 1, v и v2 равны нулю, то в эти уравнения движения для п, и п  интеграл столкновений явно не входит. Решение самого уравнения Больцмана ищется в виде
интеграл столкновений явно не входит. Решение самого уравнения Больцмана ищется в виде 
 интегралом столкновений. Неоднородная часть уравнения содержит величины n(t,r), u(t,r),
интегралом столкновений. Неоднородная часть уравнения содержит величины n(t,r), u(t,r), 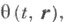 подчиненные упомянутым выше уравнениям. Таким образом, совместно рассматриваются сразу шесть уравнений. Решение уравнения для
подчиненные упомянутым выше уравнениям. Таким образом, совместно рассматриваются сразу шесть уравнений. Решение уравнения для  ищется в виде разложения по многочленам Сонина (присоединенные многочлены Лагерра полуцелого индекса) в пространстве скоростей. Для всего метода характерно, что зависимость функции распределения f(t, r, v) от времени входит только через ее зависимость от локальных величин n(t, r), u(t, r),
ищется в виде разложения по многочленам Сонина (присоединенные многочлены Лагерра полуцелого индекса) в пространстве скоростей. Для всего метода характерно, что зависимость функции распределения f(t, r, v) от времени входит только через ее зависимость от локальных величин n(t, r), u(t, r),  Нулевое приближение f=f лок определяет уравнения гидродинамики идеальной жидкости (уравнения Эйлера), к-рые являются условием существования первого приближения для f, ему же соответствуют уже уравнения Навье-Стокса с явными выражениями для коэффициентов диффузии, теплопроводности и двух вязкостен, следующий шаг - уравнение Бэрнетта и т. д. Параметром разложения является, по существу, относительное изменение величин n(t, r), u(t, r),
Нулевое приближение f=f лок определяет уравнения гидродинамики идеальной жидкости (уравнения Эйлера), к-рые являются условием существования первого приближения для f, ему же соответствуют уже уравнения Навье-Стокса с явными выражениями для коэффициентов диффузии, теплопроводности и двух вязкостен, следующий шаг - уравнение Бэрнетта и т. д. Параметром разложения является, по существу, относительное изменение величин n(t, r), u(t, r), на интервале, равном средней длине свободного пробега (параметр неоднородности), поэтому для задач со скачками этих величин (ударные волны и т. п.) метод не может быть использован.
на интервале, равном средней длине свободного пробега (параметр неоднородности), поэтому для задач со скачками этих величин (ударные волны и т. п.) метод не может быть использован.  по компонентам скорости V(что фактически эквивалентно разложению функции по многочленам Эрмита в трехмерном пространстве скоростей) с зависящими от tи rкоэффициентами, являющимися моментами искомой функции распределения, к-рые и определяются с помощью уравнения Больцмана. Первое приближение для f (приводящее к уравнениям Навье- Стокса) содержит только вторые производные от f лок.
по компонентам скорости V(что фактически эквивалентно разложению функции по многочленам Эрмита в трехмерном пространстве скоростей) с зависящими от tи rкоэффициентами, являющимися моментами искомой функции распределения, к-рые и определяются с помощью уравнения Больцмана. Первое приближение для f (приводящее к уравнениям Навье- Стокса) содержит только вторые производные от f лок.