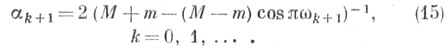"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕБЫШЕВСКИЙ ИТЕРАЦИОННЫЙ МЕТОД
Значение ЧЕБЫШЕВСКИЙ ИТЕРАЦИОННЫЙ МЕТОД в математической энциклопедии:
итерационный алгоритм нахождения решения линейного уравнения

учитывающий информацию о принадлежности Sр(A) - спектра оператора А - нек-рому множеству  и использующий свойства и параметры многочленов, наименее отклоняющихся от нуля на множестве
и использующий свойства и параметры многочленов, наименее отклоняющихся от нуля на множестве  и равных единице в нуле.
и равных единице в нуле.
Наибольшее развитие Ч. и. м. получил, когда в уравнении (1) А - линейный самосопряженный оператор и  где 0<m<М - точные границы спектра; тогда Ч. и. м. использует свойства многочленов Чебышева 1-го рода Т п (х). Для этого случая рассматривают два типа Ч. и. м.:
где 0<m<М - точные границы спектра; тогда Ч. и. м. использует свойства многочленов Чебышева 1-го рода Т п (х). Для этого случая рассматривают два типа Ч. и. м.:
 в к-рых но заданному u0 образуют последовательность
в к-рых но заданному u0 образуют последовательность 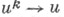 при
при  В (2), (3)
В (2), (3)  -числовые параметры методов. Если
-числовые параметры методов. Если  то начальная ошибка
то начальная ошибка  и ошибка на N- йитерации
и ошибка на N- йитерации  будут связаны формулой
будут связаны формулой
 где
где

Многочлены PN(t) вычисляют по параметрам каждого из методов (2), (3): для метода (2)
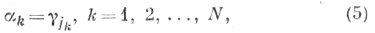
где  -элементы перестановки
-элементы перестановки 
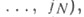 а для метода (3) - из рекуррентных соотношений
а для метода (3) - из рекуррентных соотношений

При этом

Оптимизация методов (2), (3) на классе задач, у к-рых  заключается в таком выборе параметров, чтобы PN(t)вида (4) был многочленом, наименее отклоняющимся от нуля на [m, М].П. Л. Чебышевым в 1881 было показано, что это будет многочлен
заключается в таком выборе параметров, чтобы PN(t)вида (4) был многочленом, наименее отклоняющимся от нуля на [m, М].П. Л. Чебышевым в 1881 было показано, что это будет многочлен

где  Тогда
Тогда

где

Подставляя (7) при N = k-1, k, k+1 в (6), определяют параметры  метода (3):
метода (3):

где

Таким образом, вычисляя  по формулам (9), (10), получают Ч. и. м. (3), к-рый при любом
по формулам (9), (10), получают Ч. и. м. (3), к-рый при любом  оптимально уменьшает
оптимально уменьшает 
В оптимальном методе (2) для заданного . параметры  выбирают в соответствии с перестановкой
выбирают в соответствии с перестановкой  по формуле (5) так, чтобы было (7), т. е.
по формуле (5) так, чтобы было (7), т. е.

Тогда после Nитераций для  будет справедливо неравенство (8).
будет справедливо неравенство (8).
Важной проблемой при малых т/M является вопрос об устойчивости метода (2), (5), (11). Неосмотрительный выбор  может привести к катастрофич. возрастанию
может привести к катастрофич. возрастанию  для нек-рых
для нек-рых  к потере значащих цифр, к возрастанию ошибок округления, допущенных на промежуточных итерациях. Известны алгоритмы, перемешивающие параметры (11) и гарантирующие устойчивый счет: для N= 2p см. ст. Итерационный алгоритм, а для N =3p один из алгоритмов построения
к потере значащих цифр, к возрастанию ошибок округления, допущенных на промежуточных итерациях. Известны алгоритмы, перемешивающие параметры (11) и гарантирующие устойчивый счет: для N= 2p см. ст. Итерационный алгоритм, а для N =3p один из алгоритмов построения  следующий: пусть
следующий: пусть  а
а 
 -построена, тогда образуют по правилу
-построена, тогда образуют по правилу

Существует класс методов (2) - устойчивые бесконечно продолжаемые оптимальные Ч. и. м. - позволяющих продолжить метод (2), (5), (11) после Nитераций так, чтобы он был устойчив и вновь становился оптимальным для нек-рой последовательности 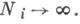 Для случая Ni =3iN из представления
Для случая Ni =3iN из представления
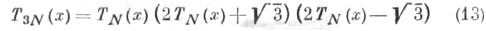
видно, что треть параметров P3N (t) совпадает с (11). Если после Nитераций продолжить итерации (2), (5), (11) далее, взяв в (11) за  2Nзначений:
2Nзначений:

то снова получается после 3Nитераций Ч. и. м. Для обеспечения устойчивости множество (14) разбивают на два: к i-му, i= 1, 2, относят те 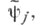 для к-рых
для к-рых  является корнем i-й скобки в (13); внутри каждого из подмножеств
является корнем i-й скобки в (13); внутри каждого из подмножеств  перемешивают с помощью перестановки
перемешивают с помощью перестановки  При N <k <2Nупотребляют в (5), (11) элементы первого множества, при
При N <k <2Nупотребляют в (5), (11) элементы первого множества, при  - второго, тем самым определяется перестановка
- второго, тем самым определяется перестановка  Продолжив аналогичным образом процесс образования параметров, получают бесконечную равномерно распределенную на [0, 1] последовательность
Продолжив аналогичным образом процесс образования параметров, получают бесконечную равномерно распределенную на [0, 1] последовательность  наз. T-последовательностью, для к-poй метод [2] становится оптимальным при Ni = 3iN и
наз. T-последовательностью, для к-poй метод [2] становится оптимальным при Ni = 3iN и
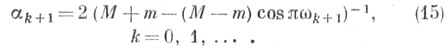
Теория Ч. и. м. (2), (3) может быть распространена на нек-рый класс несамосопряженных операторов, когда Sp Алежит на нескольких отрезках или внутри нескольких специальной формы областей (в частности, эллипса), или, когда известна информация о распределении начальной ошибки, на случай комбинированных с, методом сопряженных градиентов Ч. и. м., на задачи частичной проблемы собственных значений.
Одним из аффективных приемов ускорения сходимости итераций (2), (3) является предварительное преобразование уравнения (1) к эквивалентному уравнению вида
BAu = Bf,
и применение уже к этому уравнению Ч. и. м. Оператор Вопределяют, руководствуясь двумя факторами: 1) чтобы алгоритм вычисления величин вида Bv был нетрудоемким, 2) чтобы Sр( ВA) принадлежал множеству, для к-рого обеспечена быстрая сходимость Ч. и. м.
Лит.:[1] Марчук Г. И., Лебедев В. И., Численные методы в теории переноса нейтронов, 2 изд., М., 1981; [2] Бахвалов Н. С., Численные методы, 2 изд., М., 1975; [3] Марчук Г. И., Методы вычислительной математики, 2 изд., М., 1980; [4] Самарский А. А., Теория разностных схем, М., 1977; [5] Лебедев В. И., Финогенов С. А., лЖ. вычисл. матем. и матем. физ.


 и использующий свойства и параметры многочленов, наименее отклоняющихся от нуля на множестве
и использующий свойства и параметры многочленов, наименее отклоняющихся от нуля на множестве  и равных единице в нуле.
и равных единице в нуле.  где 0<m<М - точные границы спектра; тогда Ч. и. м. использует свойства многочленов Чебышева 1-го рода Т п (х). Для этого случая рассматривают два типа Ч. и. м.:
где 0<m<М - точные границы спектра; тогда Ч. и. м. использует свойства многочленов Чебышева 1-го рода Т п (х). Для этого случая рассматривают два типа Ч. и. м.:  в к-рых но заданному u0 образуют последовательность
в к-рых но заданному u0 образуют последовательность 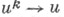 при
при  В (2), (3)
В (2), (3)  -числовые параметры методов. Если
-числовые параметры методов. Если  то начальная ошибка
то начальная ошибка  и ошибка на N- йитерации
и ошибка на N- йитерации  будут связаны формулой
будут связаны формулой  где
где 
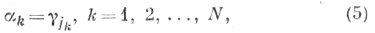
 -элементы перестановки
-элементы перестановки 
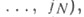 а для метода (3) - из рекуррентных соотношений
а для метода (3) - из рекуррентных соотношений 

 заключается в таком выборе параметров, чтобы PN(t)вида (4) был многочленом, наименее отклоняющимся от нуля на [m, М].П. Л. Чебышевым в 1881 было показано, что это будет многочлен
заключается в таком выборе параметров, чтобы PN(t)вида (4) был многочленом, наименее отклоняющимся от нуля на [m, М].П. Л. Чебышевым в 1881 было показано, что это будет многочлен 
 Тогда
Тогда 

 метода (3):
метода (3): 

 по формулам (9), (10), получают Ч. и. м. (3), к-рый при любом
по формулам (9), (10), получают Ч. и. м. (3), к-рый при любом  оптимально уменьшает
оптимально уменьшает 
 выбирают в соответствии с перестановкой
выбирают в соответствии с перестановкой  по формуле (5) так, чтобы было (7), т. е.
по формуле (5) так, чтобы было (7), т. е. 
 будет справедливо неравенство (8).
будет справедливо неравенство (8).  может привести к катастрофич. возрастанию
может привести к катастрофич. возрастанию  для нек-рых
для нек-рых  к потере значащих цифр, к возрастанию ошибок округления, допущенных на промежуточных итерациях. Известны алгоритмы, перемешивающие параметры (11) и гарантирующие устойчивый счет: для N= 2p см. ст. Итерационный алгоритм, а для N =3p один из алгоритмов построения
к потере значащих цифр, к возрастанию ошибок округления, допущенных на промежуточных итерациях. Известны алгоритмы, перемешивающие параметры (11) и гарантирующие устойчивый счет: для N= 2p см. ст. Итерационный алгоритм, а для N =3p один из алгоритмов построения  следующий: пусть
следующий: пусть  а
а 
 -построена, тогда образуют по правилу
-построена, тогда образуют по правилу 
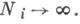 Для случая Ni =3iN из представления
Для случая Ni =3iN из представления 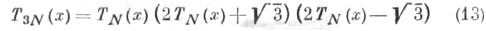
 2Nзначений:
2Nзначений: 
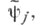 для к-рых
для к-рых  является корнем i-й скобки в (13); внутри каждого из подмножеств
является корнем i-й скобки в (13); внутри каждого из подмножеств  перемешивают с помощью перестановки
перемешивают с помощью перестановки  При N <k <2Nупотребляют в (5), (11) элементы первого множества, при
При N <k <2Nупотребляют в (5), (11) элементы первого множества, при  - второго, тем самым определяется перестановка
- второго, тем самым определяется перестановка  Продолжив аналогичным образом процесс образования параметров, получают бесконечную равномерно распределенную на [0, 1] последовательность
Продолжив аналогичным образом процесс образования параметров, получают бесконечную равномерно распределенную на [0, 1] последовательность  наз. T-последовательностью, для к-poй метод [2] становится оптимальным при Ni = 3iN и
наз. T-последовательностью, для к-poй метод [2] становится оптимальным при Ni = 3iN и