" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ЧЕБЫШЕВА ФУНКЦИИ

Значение ЧЕБЫШЕВА ФУНКЦИИ в математической энциклопедии:

- функции положительного аргумента х, определяемые следующим образом:

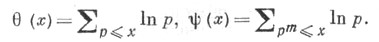
Первая сумма берется по всем простым числам а вторая - по всем положительным целым степеням простых чисел р, таким, что Функция может быть выражена через Манголъдта функцию

Из определения функций и следует, что величина равна произведению всех простых чисел а величина равна наименьшему общему кратному всех положительных целых чисел Функции и связаны между собой соотношением

Эти функции тесно связаны также с функцией

указывающей количество простых чисел

Лит.:[1] Чебышев П. Л., Избр. труды, М., 1955, с. 33-54.

С. А. Степанов.