|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕБЫШЕВА ТЕОРЕМЫЗначение ЧЕБЫШЕВА ТЕОРЕМЫ в математической энциклопедии: о простых числах - теоремы 1)-8) о распределении простых чисел, доказанные П. Л. Чебышевым [1] в 1848-50.
1) Для любого тсумма ряда
2) Как бы ни было мало а>0, a т велико, функция
3) Частное 4) Если функция
5) Для x>1 при 6) Для х, начиная с нек-рого х 0. имеют место неравенства 7) Существуют постоянные a > 0, .>0 такие, что n-е простое число Р п, для всех п =1, 2, ... удовлетворяет неравенствам anln .< Р n < Anln n. 8) В интервале ( а,2a-2) при а>3 лежит, по крайней мере, одно простое число (постулат Бертрана).
Лит.:[1] Чeбышев П. Л., Полн. собр. соч., т. 1, Теория чисел, М. - Л., 1944. |
|
|
|

 - число простых чисел, не превосходящих x, т - целое
- число простых чисел, не превосходящих x, т - целое  p - простое число, ln и- натуральный логарифм и,
p - простое число, ln и- натуральный логарифм и, 


 бесконечное число раз удовлетворяет каждому из неравенств:
бесконечное число раз удовлетворяет каждому из неравенств: 
 при
при  не может иметь предела, отличного от 1.
не может иметь предела, отличного от 1.  может быть выражена до количества порядка хln-n х включительно алгебраически в х,ln х, е х, то таким выражением является выражение (*).
может быть выражена до количества порядка хln-n х включительно алгебраически в х,ln х, е х, то таким выражением является выражение (*).  и
и 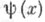 - Чебышева функции
- Чебышева функции 
 и n-го простого числа Р п. Точнее, он доказал:
и n-го простого числа Р п. Точнее, он доказал:  имеют место неравенства
имеют место неравенства 


 В основе метода вывода 5)-8) лежит тождество Чебышева:
В основе метода вывода 5)-8) лежит тождество Чебышева: 