"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ВАЛЛЕ ПУССЕНА ПРОИЗВОДНАЯЗначение ВАЛЛЕ ПУССЕНА ПРОИЗВОДНАЯ в математической энциклопедии:
обобщенная симметрическая производная; определена Ш. Балле Пуссеном [1]. Пусть г - четное и пусть существует  такое, что для всех такое, что для всех 

где  - постоянные, - постоянные,  при при  и и  Тогда число Тогда число 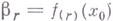 наз. производной Балле Пуссена порядка r, иначе - симметрической производной порядка rфункции f в точке x0. Аналогично определяется В. П. п. нечетного порядка r с заменой равенства (*) на наз. производной Балле Пуссена порядка r, иначе - симметрической производной порядка rфункции f в точке x0. Аналогично определяется В. П. п. нечетного порядка r с заменой равенства (*) на

В. П. п. совпадает со второй производной Римана, к-рую часто наз. производной Шварца. Если существует совпадает со второй производной Римана, к-рую часто наз. производной Шварца. Если существует  , то существует и , то существует и  ; при этом ; при этом  может не существовать. Если существует конечная обычная двусторонняя производная может не существовать. Если существует конечная обычная двусторонняя производная  , то , то  . Для функции . Для функции  , напр., , напр.,  и не существуют конечные и не существуют конечные  Если существует В. П. п. Если существует В. П. п.  , то ряд , то ряд  , полученный из ряда Фурье функции f почленным дифференцированием r раз, суммируем в точке , полученный из ряда Фурье функции f почленным дифференцированием r раз, суммируем в точке  методом методом  при при  [2] (см. Чезаро методы суммирования). [2] (см. Чезаро методы суммирования).
Лит.:[1] Lа ValleеPoussin С h. J., "Bull. Acad. de Belgique", 1908, t. 3, p. 193-254; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., М., 1965, гл. 11.
А. А. Конюшков.
|

 такое, что для всех
такое, что для всех 

 - постоянные,
- постоянные,  при
при  и
и  Тогда число
Тогда число 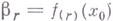 наз. производной Балле Пуссена порядка r, иначе - симметрической производной порядка rфункции f в точке x0. Аналогично определяется В. П. п. нечетного порядка r с заменой равенства (*) на
наз. производной Балле Пуссена порядка r, иначе - симметрической производной порядка rфункции f в точке x0. Аналогично определяется В. П. п. нечетного порядка r с заменой равенства (*) на 
 совпадает со второй производной Римана, к-рую часто наз. производной Шварца. Если существует
совпадает со второй производной Римана, к-рую часто наз. производной Шварца. Если существует  , то существует и
, то существует и  ; при этом
; при этом  может не существовать. Если существует конечная обычная двусторонняя производная
может не существовать. Если существует конечная обычная двусторонняя производная  , то
, то  . Для функции
. Для функции  , напр.,
, напр.,  и не существуют конечные
и не существуют конечные  Если существует В. П. п.
Если существует В. П. п.  , то ряд
, то ряд  , полученный из ряда Фурье функции f почленным дифференцированием r раз, суммируем в точке
, полученный из ряда Фурье функции f почленным дифференцированием r раз, суммируем в точке  методом
методом  при
при  [2] (см. Чезаро методы суммирования).
[2] (см. Чезаро методы суммирования).