"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕБЫШЕВА НЕРАВЕНСТВО
Значение ЧЕБЫШЕВА НЕРАВЕНСТВО в математической энциклопедии:
неравенство Бьенеме - Чебышева,- неравенство теории вероятностей, дающее оценку вероятности отклонений значений случайной величины от ее математич. ожидания через ее дисперсию. Пусть  - нек-рая случайная величина с конечными математич. ожиданием
- нек-рая случайная величина с конечными математич. ожиданием 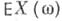 и дисперсией
и дисперсией  Ч. н. состоит в том, что для любого
Ч. н. состоит в том, что для любого  вероятность события
вероятность события

не превосходит 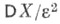 или
или

Это неравенство было независимым образом открыто И. Бьенеме (I. Bienayme, 1853) и П. Л. Чебышевым (1866). В современной литературе это неравенство чаще наз. Ч. н., возможно, и потому, что С именем П. Л. Чебышева связано использование его при доказательстве обобщения больших чисел закона (теоремы Чебышева). Ч. н. является представителем целого класса однотипных неравенств, простейшее из к-рых утверждает, что для неотрицательной случайной величины Xс конечным математич. ожиданием 

(иногда наз. неравенством Маркова). Из этого неравенства вытекают неравенства для произвольных случайных величин, зависящие от моментов:

(при r=2 и само Ч. н.), а также более общее неравенство

для неотрицательной четной неубывающей при положительных значениях хфункции f(x). Неравенство (3) указывает путь получения новых неравенств того же типа, напр. экспоненциального неравенства:

Сложилась традиция относить все эти неравенства к чебышевскому типу и даже наз. Ч. н. Существует общий принцип получения Ч. н. при определенных условиях на моменты, основанный на использовании системы многочленов Чебышева (см. [4]). Для произвольных случайных величин Ч. н. дают точные, неулучшаемые оценки, однако в нек-рых конкретных ситуациях эти оценки можно уточнить. Напр., если Xимеет унимодальное распределение с модой  совпадающей с математич. ожиданием, то справедливо неравенство Гаусса:
совпадающей с математич. ожиданием, то справедливо неравенство Гаусса:
 где
где 
Значение Ч. п. в теории вероятностен определяется в конечном счете не его точностью, а простотой и универсальностью. Большую роль Ч. н. и ого видоизменения сыграли применительно к суммам случайных величин при доказательстве различных форм закона больших чисел и закона повторного логарифма. Ч. н. для сумм независимых случайных величия было подвергнуто обобщению и уточнению в двух главных направлениях. Первое из них связано с переходом от Ч. н.

к значительно более сильному неравенству

к-рое было доказано А. II. Колмогоровым и использовано им при доказательстве больших чисел усиленного закона (см. Колмогорова неравенство).
Второе направление посвящено замене степенной оценки в Ч. н. на экспоненциально убывающую и приводит к неравенствам Бернштейна- Колмогорова:

где

(см. Берпштейна неравенство). Такие уточнения Ч. н. получаются при дополнительных условиях ограниченности слагаемых Xi.
Получены многомерные аналоги нек-рых из указанных здесь неравенств (см. [5]).
Лит.:[1] Чебышев И. Л., лМатем. сб.

 - нек-рая случайная величина с конечными математич. ожиданием
- нек-рая случайная величина с конечными математич. ожиданием 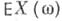 и дисперсией
и дисперсией  Ч. н. состоит в том, что для любого
Ч. н. состоит в том, что для любого  вероятность события
вероятность события 
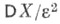 или
или 





 совпадающей с математич. ожиданием, то справедливо неравенство Гаусса:
совпадающей с математич. ожиданием, то справедливо неравенство Гаусса:  где
где 



