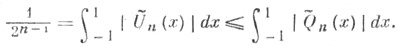|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЧЕБЫШЕВА МНОГОЧЛЕНЫЗначение ЧЕБЫШЕВА МНОГОЧЛЕНЫ в математической энциклопедии: первого рода - многочлены, ортогональные на отрезке [-1, 1] с весовой функцией Для стандартизованных Ч. м. справедливы формула
T0 (x) = 1, T1(x) = x, Т2 (х)=2х 2-1, T3(x) = 4x3 - З х, T4(x) = 8x4 - 8x2 + 1, Т 5 (х)= 16x5 - 20x3 + 5 х, ....
Старший коэффициент многочлена Т n (х) при
Нули многочлена Т п(x), определяемые равенством
Многочлен
С другой стороны, для всякого многочлена Qn(x) степени не выше и, удовлетворяющего условию
Если же функция f(х)непрерывно дифференцируема рраз на отрезке [-1, 1], причем ее р-я производная f (Р) (х) удовлетворяет условию Липшица порядка
Эти многочлены ортогональны на отрезке [-1, 1] с весовой функцией Для всякого многочлена Ч. м. были введены в 1854 П. Л. Чебышевым (см. [1]). Лит.:[1] Чебышев П. Л., Полн. собр. соч., т. 2, М.- Л., 1947, с. 23-51; [2] Сегё Г., Ортогональные многочлены, пер. с англ., М., 1962. |
|
|
|

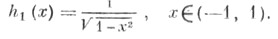
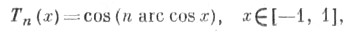
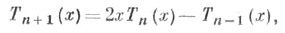
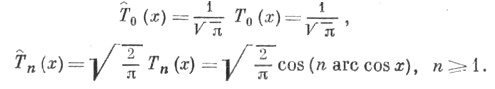
 равен 2n-1. Поэтому Ч. п. с единичным старшим коэффициентом определяются формулой
равен 2n-1. Поэтому Ч. п. с единичным старшим коэффициентом определяются формулой 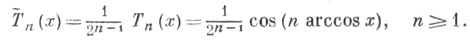
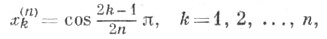

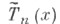 наименее отклоняется от нуля на отрезке [-1, 1], т. е. для всякого другого многочлена
наименее отклоняется от нуля на отрезке [-1, 1], т. е. для всякого другого многочлена 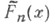 степени пс единичным старшим коэффициентом выполняется условие
степени пс единичным старшим коэффициентом выполняется условие 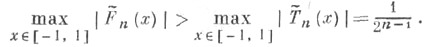
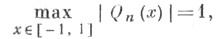 при любом
при любом 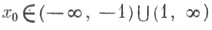 имеет место неравенство
имеет место неравенство 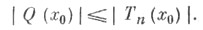
 удовлетворяет условию Дини
удовлетворяет условию Дини 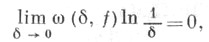 то эта функция разлагается в ряд Фурье - Чебышева
то эта функция разлагается в ряд Фурье - Чебышева 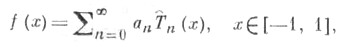 сходящийся равномерно на отрезке [-1, 1]. Коэффициенты этого ряда определяются по формуле
сходящийся равномерно на отрезке [-1, 1]. Коэффициенты этого ряда определяются по формуле 
 т. е.
т. е.  то имеет место неравенство
то имеет место неравенство  где постоянная с 1 не зависит от пи х.
где постоянная с 1 не зависит от пи х. 
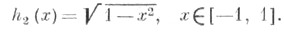
 с единичным старшим коэффициентом справедливо неравенство
с единичным старшим коэффициентом справедливо неравенство