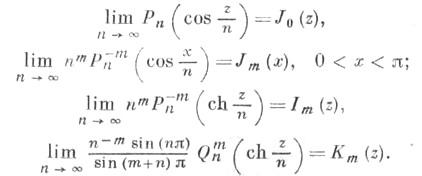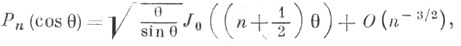|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИЗначение ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ в математической энциклопедии: бесселевы функции,- решения Zv дифференциального уравнения Бесселя
Цилиндрические функции произвольного порядка.
Ряд в правой части для
Если же v - целое, то
Важны для приложений и другие решения уравне ния (1) - Ц. ф. 3-го рода (или Ганкеля функции).
Для действительных z = x и ш функции Ганкеля являются комплексно сопряженными решениями уравнения (1). При этом функции Jv(z)дают действительную часть, а функции Nv(x). мнимую часть функций Ганкеля.
Каждая пара функций
и Мaкдoналъда функции: Эти функции являются решениями дифференциального уравнения
Цилиндрические функции целых и полуцелых порядков. Если v=n - целое число, то Jn(z) можно определить с помощью формулы Якоби - Ангера
Справедливы равенства Функция Jn(z)есть целая трансцендентная функция аргумента z;для алгебраического z = a,
в частности
в частности Интегральные представления цилиндрических функций. Для v=n=0,1,2,... имеется интегральное представление Бесселя
Для
Кроме этих представлений, существует много других интегральных представлений, в частности в виде контурных интегралов (см. [2], [4], [5]). Асимптотическое поведение цилиндрических функций. Для
Для действительных z=x имеют место
Для
Для
Нули цилиндрических функций. Нули, произвольной Ц. ф. являются простыми нулями за исключением z = 0. Если а, b, v - действительные, то между двумя действительными нулями Jn(z) лежит один действительный нуль аJn(z)+bNv(z). При действительном v Jn(z) имеет бесконечно много действительных нулей; для v>-1 все нули Jv(z) действительны; если 0<jv, 1 < jv,2 < ....-положительные нули Jn(z), то 0 < jv, 1 < jv+1, 1 < jv, 2 < jv+1,21 < jv, 3 < ...... Для v>0 справедливо jv,1>0 ; также для наименьшего положительного нуля функции J'v(z) имеет место j'v, 1> 0. Пары функций Теоремы сложения и разложения в ряды по цилиндрическим функциям. Справедливы следующие теоремы сложения:
При этом асимптотич. представления сферич. функций связаны с Ц. ф., и наоборот, как, напр., в формуле Xильба:
Вычисление значений Ц. ф. на ЭВМ. Дли вычислений значений функций J0(x), J1(x), N0(x), N1(x), I0(x), I1(x), K0(x), K1(x) удобны аппроксимации многочленами и рациональными функциями (см. [5]). О разложениях по многочленам Чебышена см. [6]. Для вычисления функций больших целых порядков, особенно на ЭВМ, применяются рекуррентные соотношения (5) -(7) (см. [5]). Лит.:[1] Ватсон Дж. Н., Теория бесселевых функций, пер. с англ., ч. 1, М., 1949; [2] Бейтмен Г., Эрдейи А.,Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены, пер. с англ., М., 1974; [3] Лебедев Н. Н., Специальные функции и их приложения, 2 изд., М.-Л., 1963; [4] Градштеейн И. С., Рыжик И. М., Таблицы интегралов, сумм, рядов и произведений, Г
|
|
|
|




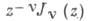 сходится абсолютно и равномерно при всех
сходится абсолютно и равномерно при всех 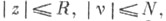 где Rи N - произвольные положительные числа. Функции
где Rи N - произвольные положительные числа. Функции 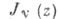 и
и  -аналитические, с особыми точками z = 0 и
-аналитические, с особыми точками z = 0 и  производные
производные 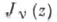 и
и  удовлетворяют следующему тождеству:
удовлетворяют следующему тождеству: 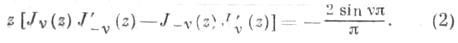
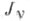 и
и  линейно зависимы, и их линейная комбинация уже не является общим решением уравнения (1). Поэтому, наряду с Ц. ф. 1-го рода, вводят Ц. ф. 2-го рода Nv (z) (или Неймана Функции, функции Вeбора):
линейно зависимы, и их линейная комбинация уже не является общим решением уравнения (1). Поэтому, наряду с Ц. ф. 1-го рода, вводят Ц. ф. 2-го рода Nv (z) (или Неймана Функции, функции Вeбора): 
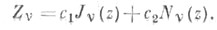
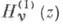 и
и  и, по определению, полагают
и, по определению, полагают  Справедливы тождества
Справедливы тождества 


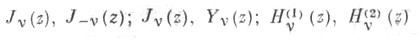


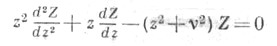

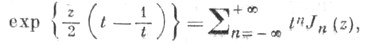
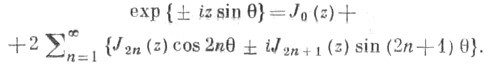

 Jn(z) есть трансцендентное число и
Jn(z) есть трансцендентное число и  при
при 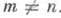

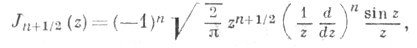
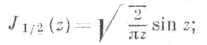

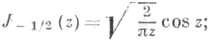
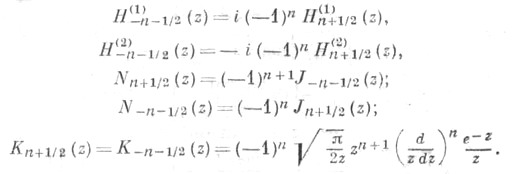
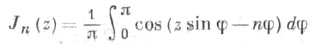

 и R(z) > 0 имеется интегральное представление Пуассона
и R(z) > 0 имеется интегральное представление Пуассона 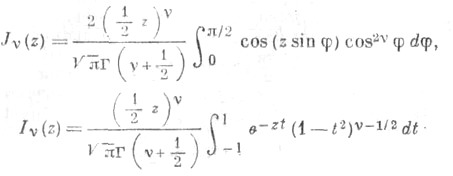


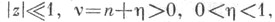 справедливо
справедливо 

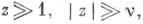 имеют место следующие оценки
имеют место следующие оценки 
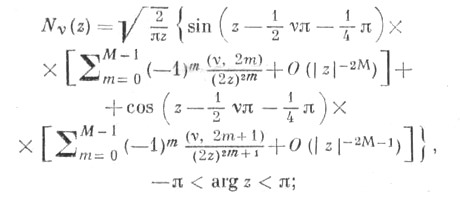

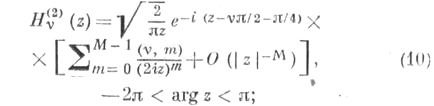
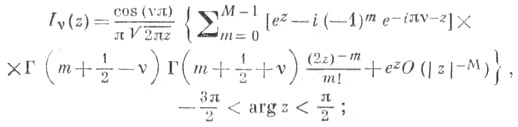
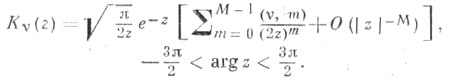
 п = 0, 1, 2, ... , ряды (9) и (10) обрываются. Функции Ганкеля являются единственными Ц. ф., к-рые стремятся к нулю для комплексных значений переменного . при
п = 0, 1, 2, ... , ряды (9) и (10) обрываются. Функции Ганкеля являются единственными Ц. ф., к-рые стремятся к нулю для комплексных значений переменного . при 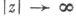 (и в этом их особое значение для приложений):
(и в этом их особое значение для приложений): 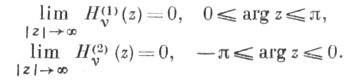

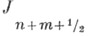 (z), п = 0, 1, 2, ..., т=1, 2, 3, ..., не имеют, кроме z = 0, общих нулей. Если
(z), п = 0, 1, 2, ..., т=1, 2, 3, ..., не имеют, кроме z = 0, общих нулей. Если 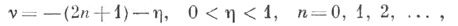 то Jv(z)имеет ровно 4n + 2 комплексных нулей, из к-рых два - чисто мнимые; если
то Jv(z)имеет ровно 4n + 2 комплексных нулей, из к-рых два - чисто мнимые; если  n=1, 2, 3, . . ., то Jv(z)имеет ровно 4n комплексных нулей с отличной от нуля действительной частью.
n=1, 2, 3, . . ., то Jv(z)имеет ровно 4n комплексных нулей с отличной от нуля действительной частью. 
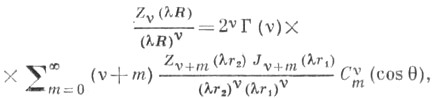
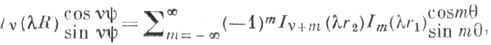
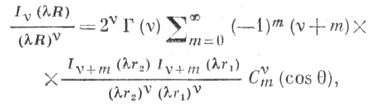
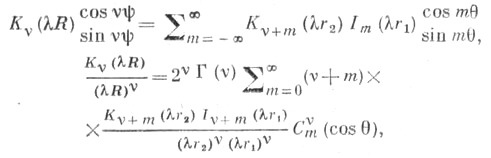
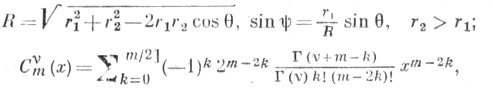
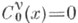 - ультрасферические многочлены. При разложении Ц. ф. используются Ломмеля многочлены, Неймана ряды, Фурье-Бесселя ряды, Дирихле ряды.
- ультрасферические многочлены. При разложении Ц. ф. используются Ломмеля многочлены, Неймана ряды, Фурье-Бесселя ряды, Дирихле ряды.