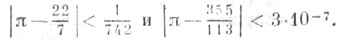"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЦЕПНАЯ ДРОБЬ
Значение ЦЕПНАЯ ДРОБЬ в математической энциклопедии:
непрерывная дробь,- выражение вида

где

и

-конечные или бесконечные последовательности комплексных чисел. Вместо выражения (1) употребляется также обозначение

Цепной дробью последовательности (2) наз. выражение вида

Для каждой Ц. д. (1) рекуррентные уравнения
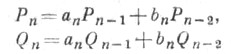
с начальными условиями

определяют две последовательности  и
и  комплексных чисел. Обычно предполагается, что последовательности (2) и (3) таковы, что
комплексных чисел. Обычно предполагается, что последовательности (2) и (3) таковы, что  для всех п,
для всех п,  Дробь
Дробь  наз. подходящей дробью порядка пЦ. д. (1). При этом
наз. подходящей дробью порядка пЦ. д. (1). При этом

кроме того
 Подходящую дробь порядка пЦ. д. последовательности (2)принято обозначать
Подходящую дробь порядка пЦ. д. последовательности (2)принято обозначать 
Для таких подходящих дробей имеют место равенства:

Если  и последовательность подходящих дробей Ц. д. (1) сходится к век-рому пределу l, то Ц. д. (1) наз. сходящейся, а число l - значением этой Ц. д. Если же
и последовательность подходящих дробей Ц. д. (1) сходится к век-рому пределу l, то Ц. д. (1) наз. сходящейся, а число l - значением этой Ц. д. Если же  т. е. Ц. д. конечна, то ее значением наз. последнюю подходящую дробь последовательности ее подходящих дробей.
т. е. Ц. д. конечна, то ее значением наз. последнюю подходящую дробь последовательности ее подходящих дробей.
Если все члены последовательностей (2) и (3), кроме, быть может, а 0, положительные действительные числа, а число а 0 действительно, то последовательность  подходящих дробей четного порядка Ц. д. (1) возрастает, п последовательность
подходящих дробей четного порядка Ц. д. (1) возрастает, п последовательность  подходящих дробей нечетного порядка убывает. При этом любая подходящая дробь четного порядка меньше каждой подходящей дроби нечетного порядка (см. [5]).
подходящих дробей нечетного порядка убывает. При этом любая подходящая дробь четного порядка меньше каждой подходящей дроби нечетного порядка (см. [5]).
Если  - такай последовательность комплексных чисел, что
- такай последовательность комплексных чисел, что  то выражение (1) наз. разложением числа в цепную дробь. Не всякая Ц. д. сходится и значение Ц. д. не всегда равно числу, разложением к-рого она является. Существует ряд признаков сходимости Ц. д. (см., напр., [3], [5]):
то выражение (1) наз. разложением числа в цепную дробь. Не всякая Ц. д. сходится и значение Ц. д. не всегда равно числу, разложением к-рого она является. Существует ряд признаков сходимости Ц. д. (см., напр., [3], [5]):
1) Пусть  все члены последовательностей (2) и (3) действительные числа и а 0>0 для всех натуральных п, начиная с нек-рого. Если для таких . выполняется неравенство
все члены последовательностей (2) и (3) действительные числа и а 0>0 для всех натуральных п, начиная с нек-рого. Если для таких . выполняется неравенство  то Ц. д. (1) сходится.
то Ц. д. (1) сходится.
2) Пусть  и все члены последовательности (2), начиная с а 1. положительны. Тогда Ц. д. последовательности (2) сходится в том и только в том случае, если ряд
и все члены последовательности (2), начиная с а 1. положительны. Тогда Ц. д. последовательности (2) сходится в том и только в том случае, если ряд  расходится (теорема Зейделя).
расходится (теорема Зейделя).
Ц. д. последовательности (2) наз. правильной, если все ее члены (кроме, быть может, а 0) - натуральные числа, а 0- целое число, а  если
если  Для любого действительного числа rсуществует единственная правильная Ц. д., значение к-рой равно r. Эта дробь конечна в том н только том случае, если число r рационально (см. [1], [2|, [4|). Алгоритм разложения действительного числа rв правильную Ц. д. определяется следующими соотношениями:
Для любого действительного числа rсуществует единственная правильная Ц. д., значение к-рой равно r. Эта дробь конечна в том н только том случае, если число r рационально (см. [1], [2|, [4|). Алгоритм разложения действительного числа rв правильную Ц. д. определяется следующими соотношениями:

где [x] означает целую часть х.
Числа а n и  определяемые из условий (4), наз. соответственно полным и неполным частными порядка празложения числа rв Ц. д.
определяемые из условий (4), наз. соответственно полным и неполным частными порядка празложения числа rв Ц. д.
В 1776 И. Ламберт (J. Lambert) нашел разложение tg xв цепную дробь:

А. Лежандр (A. Legendre) в предположении, что эта Ц. д. сходится, показал, что ее значение для рациональных значений хиррационально. Принято считать, что тем самым была доказана иррациональность числа  (см. [7]).
(см. [7]).
Л. Эйлер (L. Еuler, 1737) нашел, что

Действительное число rявляется иррациональным корнем многочлена 2-й степени с целыми коэффициентами тогда и только тогда, когда неполные частные разложения числа г в Ц. д., начиная с нек-рого, периодически повторяются (теорема Эйлера - Лагранжа, см. [1], [4]). Неизвестны (1984) разложения в правильную Ц. д. алгебраич. чисел 3-й и более высоких степеней. Не доказано и предположение, что неполные частные разложения  в Ц. д. ограничены.
в Ц. д. ограничены.
Правильные Ц. д.- весьма удобный аппарат для приближения действительных чисел рациональными. Справедливы следующие утверждения:
1) Если  и
и  - соседние подходящие дроби азложения числа r в правильную Ц. д., то
- соседние подходящие дроби азложения числа r в правильную Ц. д., то  и
и
 причем в последнем случае равенство имеет место лишь, если
причем в последнем случае равенство имеет место лишь, если 
2) Из двух соседних подходящих дробей разложения числа rв правильную Ц. д. хотя бы для одной из них выполняется неравенство:

3) Если аи b - целые числа, b>0, r - действительное число и  то
то  - подходящая дробь разложения числа r в правильную Ц. д.
- подходящая дробь разложения числа r в правильную Ц. д.
4) Если -  подходящая дробь разложения числа твправильную Ц. д., то для любых целых а и b, из b> 0,
подходящая дробь разложения числа твправильную Ц. д., то для любых целых а и b, из b> 0,  и
и
 следует b>Qn (теорема о наилучшем приближени).
следует b>Qn (теорема о наилучшем приближени).
Первые двадцать пять неполных частных разложения числа я в правильную Ц. д. суть числа: 3, 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, Г. 2, 2, 2, 2, 1, 84, 2, 1, 1.
Первые пять подходящих дробей разложения числа p в правильную Ц. д. суть:

Поэтому
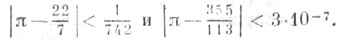
Существуют различные обобщения Ц. д. (см., напр., [9]).
Лит.:[1]Бухштаб А. А., Теория чисел, 2изд., М., 1966; [2] Венков Б. А., Элементарная теория чисел, М.-Л., 1937; [3] Марков А. А., Избранные труды, М.-Л., 1948; [4] Xинчин А. Я., Цепные дроби, 4 изд., М.-Л., 1978; [5] Xованский А. Н., Приложение цепных дробей и их обобщений к вопросам приближенного анализа, М., 1966; [6] История математики, т. 3, М., 1972; [7] О квадратуре круга, пер. с нем., 3изд., М.-Л., 1936; [8] Perron О., Die Lehre von. den Kettenbruchen, 3 Aft., Bd 1-2, Stuttg., 1954-57; [9] Szekeres O., лAnn. Univ. sci., Sec. math.






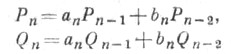

 и
и  комплексных чисел. Обычно предполагается, что последовательности (2) и (3) таковы, что
комплексных чисел. Обычно предполагается, что последовательности (2) и (3) таковы, что  для всех п,
для всех п,  Дробь
Дробь  наз. подходящей дробью порядка пЦ. д. (1). При этом
наз. подходящей дробью порядка пЦ. д. (1). При этом 
 Подходящую дробь порядка пЦ. д. последовательности (2)принято обозначать
Подходящую дробь порядка пЦ. д. последовательности (2)принято обозначать 

 и последовательность подходящих дробей Ц. д. (1) сходится к век-рому пределу l, то Ц. д. (1) наз. сходящейся, а число l - значением этой Ц. д. Если же
и последовательность подходящих дробей Ц. д. (1) сходится к век-рому пределу l, то Ц. д. (1) наз. сходящейся, а число l - значением этой Ц. д. Если же  т. е. Ц. д. конечна, то ее значением наз. последнюю подходящую дробь последовательности ее подходящих дробей.
т. е. Ц. д. конечна, то ее значением наз. последнюю подходящую дробь последовательности ее подходящих дробей.  подходящих дробей четного порядка Ц. д. (1) возрастает, п последовательность
подходящих дробей четного порядка Ц. д. (1) возрастает, п последовательность  подходящих дробей нечетного порядка убывает. При этом любая подходящая дробь четного порядка меньше каждой подходящей дроби нечетного порядка (см. [5]).
подходящих дробей нечетного порядка убывает. При этом любая подходящая дробь четного порядка меньше каждой подходящей дроби нечетного порядка (см. [5]).  - такай последовательность комплексных чисел, что
- такай последовательность комплексных чисел, что  то выражение (1) наз. разложением числа в цепную дробь. Не всякая Ц. д. сходится и значение Ц. д. не всегда равно числу, разложением к-рого она является. Существует ряд признаков сходимости Ц. д. (см., напр., [3], [5]):
то выражение (1) наз. разложением числа в цепную дробь. Не всякая Ц. д. сходится и значение Ц. д. не всегда равно числу, разложением к-рого она является. Существует ряд признаков сходимости Ц. д. (см., напр., [3], [5]):  все члены последовательностей (2) и (3) действительные числа и а 0>0 для всех натуральных п, начиная с нек-рого. Если для таких . выполняется неравенство
все члены последовательностей (2) и (3) действительные числа и а 0>0 для всех натуральных п, начиная с нек-рого. Если для таких . выполняется неравенство  то Ц. д. (1) сходится.
то Ц. д. (1) сходится.  и все члены последовательности (2), начиная с а 1. положительны. Тогда Ц. д. последовательности (2) сходится в том и только в том случае, если ряд
и все члены последовательности (2), начиная с а 1. положительны. Тогда Ц. д. последовательности (2) сходится в том и только в том случае, если ряд  расходится (теорема Зейделя).
расходится (теорема Зейделя).  если
если  Для любого действительного числа rсуществует единственная правильная Ц. д., значение к-рой равно r. Эта дробь конечна в том н только том случае, если число r рационально (см. [1], [2|, [4|). Алгоритм разложения действительного числа rв правильную Ц. д. определяется следующими соотношениями:
Для любого действительного числа rсуществует единственная правильная Ц. д., значение к-рой равно r. Эта дробь конечна в том н только том случае, если число r рационально (см. [1], [2|, [4|). Алгоритм разложения действительного числа rв правильную Ц. д. определяется следующими соотношениями: 
 определяемые из условий (4), наз. соответственно полным и неполным частными порядка празложения числа rв Ц. д.
определяемые из условий (4), наз. соответственно полным и неполным частными порядка празложения числа rв Ц. д. 
 (см. [7]).
(см. [7]). 
 в Ц. д. ограничены.
в Ц. д. ограничены.  и
и  - соседние подходящие дроби азложения числа r в правильную Ц. д., то
- соседние подходящие дроби азложения числа r в правильную Ц. д., то  и
и  причем в последнем случае равенство имеет место лишь, если
причем в последнем случае равенство имеет место лишь, если 

 то
то  - подходящая дробь разложения числа r в правильную Ц. д.
- подходящая дробь разложения числа r в правильную Ц. д.  подходящая дробь разложения числа твправильную Ц. д., то для любых целых а и b, из b> 0,
подходящая дробь разложения числа твправильную Ц. д., то для любых целых а и b, из b> 0,  и
и  следует b>Qn (теорема о наилучшем приближени).
следует b>Qn (теорема о наилучшем приближени).