"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЦЕНТРИРОВАННОЕ СЕМЕЙСТВО МНОЖЕСТВЗначение ЦЕНТРИРОВАННОЕ СЕМЕЙСТВО МНОЖЕСТВ в математической энциклопедии:
- семейство, пересечение любого конечного множества элементов к-рого не пусто. Напр., счетное семейство  состоящее из подмножеств натурального ряда чисел состоящее из подмножеств натурального ряда чисел  вида вида 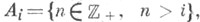 центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м. центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м.
Впервые бесконечные Ц. с. м. были использованы в общей топологии для характеристики бикомпактных пространств. Ц. с. м., замкнутых в топологич. пространстве, используются при построении его бикомпактного расширения и его абсолюта.
Понятие Ц. с. м. допускает следующее обобщение. Пусть m - бесконечное кардинальное число. Тогда m-центрированным семейством: множеств наз. такое семейство, что пересечение любого множества его элементов мощности, меньшей т, не пусто. Такие семейства применяются для характеристики m-компактных пространств и в абстрактной теории меры. Лит.:[1] Келли Дж., Общая топология, пер. с англ., 2 изд., М., 1981; [2] Gillman L., Jеrisоn M., Rings of continuons functions, Princeton. 1960.
Б. А. Ефимов.
|

 состоящее из подмножеств натурального ряда чисел
состоящее из подмножеств натурального ряда чисел  вида
вида 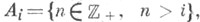 центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м.
центрировано. Центрированным будет любое семейство, пересечение всех элементов к-рого не пусто. Этим свойством обладает любое конечное Ц. с. м.