|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЭРА УМНОЖЕНИЕЗначение БЭРА УМНОЖЕНИЕ в математической энциклопедии: - бинарная операция на множестве классов эквивалентных расширений модулей; предложена Р. Бэром [1]. Пусть Л и В -произвольные модули. Расширением Ас ядром Вназ. точная последовательность: Расширение (1) наз. эквивалентным расширению если существует гомоморфизм Множество классов эквивалентных расширений обозначается два расширения. В прямой сумме выбираются подмодули И Ясно, что (2) и (3) наз. расширение Лит.:[1] Baer R., "Math. Z.", 1934, Bd 38, S. 374-416; [2] Картан А., Эйленберг С., Гомологическая алгебра, пер. с англ., М., 1960. В. Е. Говоров. ВЭРРИ - ЭССЕЕНА НЕРАВЕНСТВО - неравенство, дающее оценку отклонения функции распределения суммы независимых случайных величин от нормальной функции распределения. Пусть Пусть тогда для любого п где А - абсолютная положительная постоянная. Этот результат был получен А. Бэрри [1] и независимо от него К.-Г. Эссееном [2]. Лит.:[1] Berry А. С., "Trans. Amer. Math. Soc.", 1941, v. 49, № 1, p.122-36; [2] Esseen C.-G., "Ark. Mat., Astr. och Fysik", 1942, Bd 28A, № 9, p. 1 - 19; [3] Пeтров В. В., Суммы независимых случайных величин, М., 1972. В. В. Петров. |
|
|
|
включаемый в коммутативную диаграмму:
. Б. у. на 
индуцируется следующим образом определенной операцией произведения расширений. Пусть 
, так что определен фактормодуль 
Произведением Бэра расширений 
- независимые одинаково распределенные случайные величины такие, что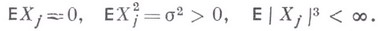 
!