" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ХЬЮИТТА РАСШИРЕНИЕ

Значение ХЬЮИТТА РАСШИРЕНИЕ в математической энциклопедии:

- расширение топологич. пространства, наибольшее относительно свойства продолжения действительных непрерывных функции; предложено Э. Хьюиттом [1].
Гомеоморфное вложение наз. функциональным расширением, если v(X)плотно в Y и для любой непрерывной функции существует такая непрерывная функция что Вполне регулярное пространство Xназ. Q-пространством, или функционально замкнутым пространством, если любое его функциональное расширение является гомеоморфизмом, т. е. v(X) = X. Функциональное расширение вполне регулярного пространства Xназ. расширением Хьюитта, если v(X)является Q-пространством. Любое вполне регулярное пространство обладает Х. <р., и последнее единственно с точностью до гомеоморфизма.
Х. <р. можно определить так же, как подпространство тех точек у Стоуна- Чеха бикомпактного расширения что любая непрерывная действительная функция 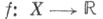продолжается на

Лит.:[1] Меwitt E., лTrans. Amer. Math. Soc.