"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХОПФА РАССЛОЕНИЕЗначение ХОПФА РАССЛОЕНИЕ в математической энциклопедии:
- локально тривиальное расслоение  при n = 2, 4, 8. Это - один из самых ранних примеров локально тривиальных расслоений, введенный X. Хопфом [1]. Эти отображения индуцируют тривиальные отображения в гомологиях и когомологиях, однако они не гомотопны нулевому отображению, что вытекает из нетривиальности Хопфа инварианта этих отображений. Для их построения потребуется т. н. конструкция Хопфа. при n = 2, 4, 8. Это - один из самых ранних примеров локально тривиальных расслоений, введенный X. Хопфом [1]. Эти отображения индуцируют тривиальные отображения в гомологиях и когомологиях, однако они не гомотопны нулевому отображению, что вытекает из нетривиальности Хопфа инварианта этих отображений. Для их построения потребуется т. н. конструкция Хопфа.
Пусть X*Y - джойн пространств . и Y, он обладает естественными координатами  где где  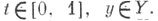 При этом X*pt = SX, где SX - надстройка над X. Конструкция Хопфа При этом X*pt = SX, где SX - надстройка над X. Конструкция Хопфа  сопоставляет отображению f: Xx Y -> Zотображение сопоставляет отображению f: Xx Y -> Zотображение   заданное соотношением заданное соотношением  
Пусть отображения  определены при n = 2, 4, 8 при помощи умножений: в комплексных числах при n = 2, в кватернионах при n = 4 и в числах Кэли при n = 8. Тогда Sn-1 * Sn-1= S2n-1, и отображением Хопфа наз. отображение определены при n = 2, 4, 8 при помощи умножений: в комплексных числах при n = 2, в кватернионах при n = 4 и в числах Кэли при n = 8. Тогда Sn-1 * Sn-1= S2n-1, и отображением Хопфа наз. отображение 
Отображение Хопфа  n =2, 4, 8 является локально тривиальным расслоением со слоем Sn-1. Если n =2, 4, 8 является локально тривиальным расслоением со слоем Sn-1. Если  - отображение бистепени (d1, d2), то инвариант Хопфа отображения - отображение бистепени (d1, d2), то инвариант Хопфа отображения 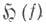 равен d1d2. В частности, инвариант Хопфа Х. <р. равен 1. равен d1d2. В частности, инвариант Хопфа Х. <р. равен 1.
Иногда Х. <р. наз. отображение  заданное формулой заданное формулой  Это отображение является локально тривиальным расслоением со слоем S1. При n = 1 получается классич. Х. <р. Это отображение является локально тривиальным расслоением со слоем S1. При n = 1 получается классич. Х. <р.  Лит.:[1] Hорf H., лFund. math.
|

 при n = 2, 4, 8. Это - один из самых ранних примеров локально тривиальных расслоений, введенный X. Хопфом [1]. Эти отображения индуцируют тривиальные отображения в гомологиях и когомологиях, однако они не гомотопны нулевому отображению, что вытекает из нетривиальности Хопфа инварианта этих отображений. Для их построения потребуется т. н. конструкция Хопфа.
при n = 2, 4, 8. Это - один из самых ранних примеров локально тривиальных расслоений, введенный X. Хопфом [1]. Эти отображения индуцируют тривиальные отображения в гомологиях и когомологиях, однако они не гомотопны нулевому отображению, что вытекает из нетривиальности Хопфа инварианта этих отображений. Для их построения потребуется т. н. конструкция Хопфа.  где
где 
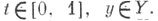 При этом X*pt = SX, где SX - надстройка над X. Конструкция Хопфа
При этом X*pt = SX, где SX - надстройка над X. Конструкция Хопфа  сопоставляет отображению f: Xx Y -> Zотображение
сопоставляет отображению f: Xx Y -> Zотображение 
 заданное соотношением
заданное соотношением 

 определены при n = 2, 4, 8 при помощи умножений: в комплексных числах при n = 2, в кватернионах при n = 4 и в числах Кэли при n = 8. Тогда Sn-1 * Sn-1= S2n-1, и отображением Хопфа наз. отображение
определены при n = 2, 4, 8 при помощи умножений: в комплексных числах при n = 2, в кватернионах при n = 4 и в числах Кэли при n = 8. Тогда Sn-1 * Sn-1= S2n-1, и отображением Хопфа наз. отображение 
 n =2, 4, 8 является локально тривиальным расслоением со слоем Sn-1. Если
n =2, 4, 8 является локально тривиальным расслоением со слоем Sn-1. Если  - отображение бистепени (d1, d2), то инвариант Хопфа отображения
- отображение бистепени (d1, d2), то инвариант Хопфа отображения 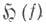 равен d1d2. В частности, инвариант Хопфа Х. <р. равен 1.
равен d1d2. В частности, инвариант Хопфа Х. <р. равен 1.  заданное формулой
заданное формулой  Это отображение является локально тривиальным расслоением со слоем S1. При n = 1 получается классич. Х. <р.
Это отображение является локально тривиальным расслоением со слоем S1. При n = 1 получается классич. Х. <р. 