"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХОДЖА ГИПОТЕЗАЗначение ХОДЖА ГИПОТЕЗА в математической энциклопедии:
- предположение о том, что для любого гладкого проективного многообразия Xнад полем 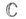 комплексных чисел и для любого целого комплексных чисел и для любого целого   -пространство -пространство  где где  - компонента типа ( р, р )в разложении Ходжа - компонента типа ( р, р )в разложении Ходжа 
порождается классами когомологий алгебраич. циклов коразмерности рна X. Эта гипотеза была выдвинута У. Ходжем [1].
В случае р = 1 Х. г. равносильна Лефшеца теореме о когомологиях типа (1,1). Х. <г. доказана также для следующих классов многообразий: 1) X - гладкое 4-мерное унилинейчатое многообразие, т. е. такое, что существует рациональное отображение конечной степени  где Y - гладкое многообразие (см. [2]). Унилинейчатыми многообразиями являются, напр., унирациональные многообразия и 4-мерные полные пересечения с обильным антикано-нич. классом (см. [3]). 2) X - гладкая гиперповерхность Ферма простой степени (см. [4], [5]). 3) X - простое 5-мерное абелево многообразие (см. [6]). 4) X-- простое d-мерное абелево многообразие, причем End где Y - гладкое многообразие (см. [2]). Унилинейчатыми многообразиями являются, напр., унирациональные многообразия и 4-мерные полные пересечения с обильным антикано-нич. классом (см. [3]). 2) X - гладкая гиперповерхность Ферма простой степени (см. [4], [5]). 3) X - простое 5-мерное абелево многообразие (см. [6]). 4) X-- простое d-мерное абелево многообразие, причем End 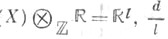 - нечетное число, или End - нечетное число, или End  -нечетное число. -нечетное число.
Лит.:[1] Ноdgе W. V. D., лProc. Intern. Congr. Math.
|

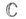 комплексных чисел и для любого целого
комплексных чисел и для любого целого 
 -пространство
-пространство  где
где  - компонента типа ( р, р )в разложении Ходжа
- компонента типа ( р, р )в разложении Ходжа 
 где Y - гладкое многообразие (см. [2]). Унилинейчатыми многообразиями являются, напр., унирациональные многообразия и 4-мерные полные пересечения с обильным антикано-нич. классом (см. [3]). 2) X - гладкая гиперповерхность Ферма простой степени (см. [4], [5]). 3) X - простое 5-мерное абелево многообразие (см. [6]). 4) X-- простое d-мерное абелево многообразие, причем End
где Y - гладкое многообразие (см. [2]). Унилинейчатыми многообразиями являются, напр., унирациональные многообразия и 4-мерные полные пересечения с обильным антикано-нич. классом (см. [3]). 2) X - гладкая гиперповерхность Ферма простой степени (см. [4], [5]). 3) X - простое 5-мерное абелево многообразие (см. [6]). 4) X-- простое d-мерное абелево многообразие, причем End 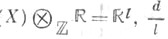 - нечетное число, или End
- нечетное число, или End  -нечетное число.
-нечетное число.