Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХИНЧИНА НЕРАВЕНСТВОЗначение ХИНЧИНА НЕРАВЕНСТВО в математической энциклопедии: для независимых функций-оценка в Lp суммы независимых функций. Пусть fk- система независимых функций и для нек-рого р> 2
Тогда Если
где
Одно из многочисленных приложений X. н.: если
Лит.:[1]Хинчин A., лMath. Z.
|
|
|
|






 при
при  Это неравенство было установлено А. Я. Хинчиным [1]. Точное значение А 1 равно 1/2.
Это неравенство было установлено А. Я. Хинчиным [1]. Точное значение А 1 равно 1/2.  что для любых элементов х k из банахова пространства Е
что для любых элементов х k из банахова пространства Е 
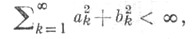
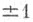 функция
функция 
 (см. [5]).
(см. [5]).