"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХАРДИ - ЛИТЛВУДА ПРОБЛЕМАЗначение ХАРДИ - ЛИТЛВУДА ПРОБЛЕМА в математической энциклопедии:
задача нахождения асимптотич. формулы для числа Q(n)решеий уравнения 
где р - простое, хи у - целые, п - натуральное число  Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения

где  - фиксированное целое число, - фиксированное целое число,
X. -Л. п. была поставлена Г. Харди (G. Hardy) и Дж. Литлвудом (J. Littlewood) в 1923 и рассмотрена ими на основе эвристич. и гипотетич. соображений.
Дисперсионный метод, разработанный Ю. В. Линником, позволил ему найти асимптотику для (1): 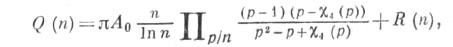
где

Из аналогичной формулы для (2) следует бесконечность множества простых чисел вида р=x2+y2+l. С помощью дисперсионного метода найдена асимптотика для числа решений обобщенного уравнения Харди - Литлвуда  где р - простое, где р - простое,  - заданная примитивная положительно определенная квадратичная форма. - заданная примитивная положительно определенная квадратичная форма.
Рассмотрение аналогичного уравнения  приводит к доказательству бесконечности множества простых чисел вида приводит к доказательству бесконечности множества простых чисел вида 
Теорема Виноградова - Бомбьери о распределении простых чисел в арифметич. прогрессиях в среднем также доставляет решение X.- Л. п., заменяя фактически расширенную гипотезу Римана теоремами типа большого решета. Лит.:[1] Линник Ю. В., Дисперсионный метод в бинарных аддитивных аадачах, Л., 1961; [2] Брeдихин Б. М., Линник Ю. В.. лМатем. сб.
|


 Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения
Аналогом этой задачи является проблема нахождения асимптотики для числа решений уравнения 
 - фиксированное целое число,
- фиксированное целое число,
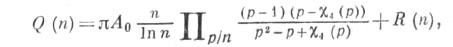

 где р - простое,
где р - простое,  - заданная примитивная положительно определенная квадратичная форма.
- заданная примитивная положительно определенная квадратичная форма.  приводит к доказательству бесконечности множества простых чисел вида
приводит к доказательству бесконечности множества простых чисел вида 