"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ
Значение ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ в математической энциклопедии:
преобразование Фурье - Стилтьеса вероятностной меры  - комплскснозначная функция, заданная на всей числовой оси
- комплскснозначная функция, заданная на всей числовой оси  формулой
формулой

X. ф. случайной величины Xпо определению есть X. ф. ее вероятностного распределения
 Метод, связанный с использованием X. ф., был впервые применен А. М. Ляпуновым и позднее стал одним из основных аналитич. методов теории вероятностей. Особенно эффективно он используется при доказательстве предельных теорем теории вероятностей, напр. доказательство центральной предельной теоремы для независимых одинаково распределенных случайных величин со 2-ми моментами сводится к элементарному соотношению
Метод, связанный с использованием X. ф., был впервые применен А. М. Ляпуновым и позднее стал одним из основных аналитич. методов теории вероятностей. Особенно эффективно он используется при доказательстве предельных теорем теории вероятностей, напр. доказательство центральной предельной теоремы для независимых одинаково распределенных случайных величин со 2-ми моментами сводится к элементарному соотношению

Основные свойства X. ф. 1)  и
и  положительно определена, т. е.
положительно определена, т. е.

для любых конечных наборов комплексных чисел  и аргументов
и аргументов 
2)  равномерно непрерывна на всей оси
равномерно непрерывна на всей оси 

4) в частности,
в частности,  принимает только действительные значения (и является четной функцией) в том и только том случае, когда соответствующее вероятностное распределение симметрично, т. е.
принимает только действительные значения (и является четной функцией) в том и только том случае, когда соответствующее вероятностное распределение симметрично, т. е.
 где
где 
5) X. ф. однозначно определяет меру; имеет место формула обращения:

для любых интервалов (а, 6), концы к-рых имеют нулевую m-меру. Если 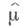 интегрируема (абсолютно, если интеграл понимать в смысле Римана) на
интегрируема (абсолютно, если интеграл понимать в смысле Римана) на  то соответствующая функция распределения имеет плотность ри
то соответствующая функция распределения имеет плотность ри

6) X. ф. свертки двух вероятностных мер (суммы двух независимых случайных величин) есть произведение их X. ф.
Следующие три свойства выражают связь между существованием моментов случайной величины и степенью гладкости ее X. ф.
7) Если  для нек-рого натурального п, то при всех натуральных
для нек-рого натурального п, то при всех натуральных  существуют производные порядка rот X. ф.
существуют производные порядка rот X. ф.  случайной величины Xи имеет место равенство
случайной величины Xи имеет место равенство

Т. о.,
8) Если существует  то
то 
9) Если  для всех пи
для всех пи

то при всех  имеет место
имеет место

Использование метода X. ф. главным образом основано на указанных выше свойствах X. ф., а также на следующих двух теоремах.
Теорема Бохнера (описание класса X. ф.). Пусть функция f задана на 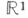 и f(0)=1. Для того чтобы f была X. ф. нек-рой вероятностной меры, необходимо и достаточно, чтобы она была непрерывна и положительно определена.
и f(0)=1. Для того чтобы f была X. ф. нек-рой вероятностной меры, необходимо и достаточно, чтобы она была непрерывна и положительно определена.
Теорема Леви (непрерывность соответствия). Пусть  -последовательность вероятностных мeр, а
-последовательность вероятностных мeр, а  -последовательность их X. ф. Тогда
-последовательность их X. ф. Тогда  слабо сходится к нек-рой вероятностной мере
слабо сходится к нек-рой вероятностной мере  (т. е.
(т. е. 
 для произвольной непрерывной ограниченной функции
для произвольной непрерывной ограниченной функции  в том п только том случае, если
в том п только том случае, если  н каждой точке
н каждой точке 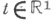 сходится к нек-рой непрерывной функции f; в случае сходимости функция
сходится к нек-рой непрерывной функции f; в случае сходимости функция  Отсюда следует, что относительная компактность (в смысле слабой сходимости) семейства вероятностных мер равносильна равностепенной непрерывности в нуле семейства соответствующих X. ф.
Отсюда следует, что относительная компактность (в смысле слабой сходимости) семейства вероятностных мер равносильна равностепенной непрерывности в нуле семейства соответствующих X. ф.
Теорема Бохнера позволяет смотреть на преобразование Фурье - Стилтьеса как на изоморфизм между полугруппой (относительно операции свертки) вероятностных мер в  и полугруппой (относительно поточечного умножения) положительно определенных непрерывных равных в нуле единице функций на
и полугруппой (относительно поточечного умножения) положительно определенных непрерывных равных в нуле единице функций на  Теорема Леви утверждает, что этот алгебраич. изоморфизм является и топологич. гомеоморфизмом, если в полугруппе вероятностных мер иметь в виду топологию слабой сходимости, а в полугруппе положительно определенных функций - топологию равномерной сходимости на ограниченных множествах.
Теорема Леви утверждает, что этот алгебраич. изоморфизм является и топологич. гомеоморфизмом, если в полугруппе вероятностных мер иметь в виду топологию слабой сходимости, а в полугруппе положительно определенных функций - топологию равномерной сходимости на ограниченных множествах.
Известны выражения X. ф. основных вероятностных мор (см. [1], [2]), напр., X. ф. гауссовой меры со средним ти дисперсией 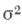 есть
есть 
Для неотрицательных целочисленных случайных величин X, наряду с X. ф., используется ее аналог - производящая функция

связанная с X. ф. соотношением 
X. ф. вероятностной меры  в конечномерном пространстве
в конечномерном пространстве  определяется аналогично:
определяется аналогично:

где <t, х> означает скалярное произведение. Сформулированные выше факты справедливы и для X. ф. вероятностных мер в 
Лит.:[1] Лукач Е., Характеристические функции, пер. с англ., М., 1979; [2] Феллер В., Введение в теорию вероятностей и ее приложения, т. 2. пер. с англ., М., 1967; [3] Прохоров Ю. В., Розанов Ю. А., Теория вероятностей. Основные понятия. Предельные теоремы. Случайные процессы, 2 изд., М., 1973; [4] 3олотарев В. М., Одномерные устойчивые распределения, М., 1983.
Н. H. Вахания.

 - комплскснозначная функция, заданная на всей числовой оси
- комплскснозначная функция, заданная на всей числовой оси  формулой
формулой 
 Метод, связанный с использованием X. ф., был впервые применен А. М. Ляпуновым и позднее стал одним из основных аналитич. методов теории вероятностей. Особенно эффективно он используется при доказательстве предельных теорем теории вероятностей, напр. доказательство центральной предельной теоремы для независимых одинаково распределенных случайных величин со 2-ми моментами сводится к элементарному соотношению
Метод, связанный с использованием X. ф., был впервые применен А. М. Ляпуновым и позднее стал одним из основных аналитич. методов теории вероятностей. Особенно эффективно он используется при доказательстве предельных теорем теории вероятностей, напр. доказательство центральной предельной теоремы для независимых одинаково распределенных случайных величин со 2-ми моментами сводится к элементарному соотношению 
 и
и  положительно определена, т. е.
положительно определена, т. е. 
 и аргументов
и аргументов 
 равномерно непрерывна на всей оси
равномерно непрерывна на всей оси 

 в частности,
в частности,  принимает только действительные значения (и является четной функцией) в том и только том случае, когда соответствующее вероятностное распределение симметрично, т. е.
принимает только действительные значения (и является четной функцией) в том и только том случае, когда соответствующее вероятностное распределение симметрично, т. е.
 где
где 

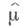 интегрируема (абсолютно, если интеграл понимать в смысле Римана) на
интегрируема (абсолютно, если интеграл понимать в смысле Римана) на  то соответствующая функция распределения имеет плотность ри
то соответствующая функция распределения имеет плотность ри 
 для нек-рого натурального п, то при всех натуральных
для нек-рого натурального п, то при всех натуральных  существуют производные порядка rот X. ф.
существуют производные порядка rот X. ф.  случайной величины Xи имеет место равенство
случайной величины Xи имеет место равенство 

 то
то 
 для всех пи
для всех пи 
 имеет место
имеет место 
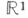 и f(0)=1. Для того чтобы f была X. ф. нек-рой вероятностной меры, необходимо и достаточно, чтобы она была непрерывна и положительно определена.
и f(0)=1. Для того чтобы f была X. ф. нек-рой вероятностной меры, необходимо и достаточно, чтобы она была непрерывна и положительно определена.  -последовательность вероятностных мeр, а
-последовательность вероятностных мeр, а  -последовательность их X. ф. Тогда
-последовательность их X. ф. Тогда  слабо сходится к нек-рой вероятностной мере
слабо сходится к нек-рой вероятностной мере  (т. е.
(т. е. 
 для произвольной непрерывной ограниченной функции
для произвольной непрерывной ограниченной функции  в том п только том случае, если
в том п только том случае, если  н каждой точке
н каждой точке 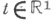 сходится к нек-рой непрерывной функции f; в случае сходимости функция
сходится к нек-рой непрерывной функции f; в случае сходимости функция  Отсюда следует, что относительная компактность (в смысле слабой сходимости) семейства вероятностных мер равносильна равностепенной непрерывности в нуле семейства соответствующих X. ф.
Отсюда следует, что относительная компактность (в смысле слабой сходимости) семейства вероятностных мер равносильна равностепенной непрерывности в нуле семейства соответствующих X. ф.  и полугруппой (относительно поточечного умножения) положительно определенных непрерывных равных в нуле единице функций на
и полугруппой (относительно поточечного умножения) положительно определенных непрерывных равных в нуле единице функций на  Теорема Леви утверждает, что этот алгебраич. изоморфизм является и топологич. гомеоморфизмом, если в полугруппе вероятностных мер иметь в виду топологию слабой сходимости, а в полугруппе положительно определенных функций - топологию равномерной сходимости на ограниченных множествах.
Теорема Леви утверждает, что этот алгебраич. изоморфизм является и топологич. гомеоморфизмом, если в полугруппе вероятностных мер иметь в виду топологию слабой сходимости, а в полугруппе положительно определенных функций - топологию равномерной сходимости на ограниченных множествах. 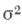 есть
есть 


 в конечномерном пространстве
в конечномерном пространстве  определяется аналогично:
определяется аналогично: 
