"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХАРАКТЕРЗначение ХАРАКТЕР в математической энциклопедии:
представления p ассоциативной алгебры А- функция j на алгебре А, определенная формулой  для для  где где 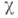 - линейный функционал, определенный на нек-ром идеале I в алгебре - линейный функционал, определенный на нек-ром идеале I в алгебре  и удовлетворяющий условию и удовлетворяющий условию  для всех для всех  Если представление Если представление  конечномерно или если алгебра конечномерно или если алгебра  содержит ненулевой конечномерный оператор, то в качестве содержит ненулевой конечномерный оператор, то в качестве  обычно рассматривается след оператора. Пусть Aесть С*-алгебра, обычно рассматривается след оператора. Пусть Aесть С*-алгебра,  -такое представление С*-алгебры А, что Неймана алгебра -такое представление С*-алгебры А, что Неймана алгебра  порожденная алгеброй порожденная алгеброй  является фактором полуконечного типа; пусть является фактором полуконечного типа; пусть  -точный нормальный полуконечный след на -точный нормальный полуконечный след на  -линейное продолжение следа -линейное продолжение следа  на идеал на идеал  если множество если множество  отлично от нуля, то формула отлично от нуля, то формула  определяет X. представления алгебры А, ограничение к-рого на А + есть характер С*-алгебры А. Во многих случаях X. представления алгебры определяет представление однозначно с точностью до нек-рого отношения эквивалентности; напр., характер неприводимого конечномерного представления определяет представление однозначно с точностью до эквивалентности; X. фактор представления С*-алгебры, допускающего след, определяет представление однозначно с точностью до квазиэквивалеитности. определяет X. представления алгебры А, ограничение к-рого на А + есть характер С*-алгебры А. Во многих случаях X. представления алгебры определяет представление однозначно с точностью до нек-рого отношения эквивалентности; напр., характер неприводимого конечномерного представления определяет представление однозначно с точностью до эквивалентности; X. фактор представления С*-алгебры, допускающего след, определяет представление однозначно с точностью до квазиэквивалеитности. Лит.:[1] Кириллов А. А., Элементы теории представлений, 2 изд., М., 1978; [2] Кэртис Ч., Райнер И., Теория представлений конечных групп и ассоциативных алгебр, пер. с англ., М., 1969; [3] Диксмье Ж., С*-алгебры и их представления, пер. с франц., М., 1974.
А. И. Штерн.
|

 для
для  где
где 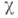 - линейный функционал, определенный на нек-ром идеале I в алгебре
- линейный функционал, определенный на нек-ром идеале I в алгебре  и удовлетворяющий условию
и удовлетворяющий условию  для всех
для всех  Если представление
Если представление  конечномерно или если алгебра
конечномерно или если алгебра  содержит ненулевой конечномерный оператор, то в качестве
содержит ненулевой конечномерный оператор, то в качестве  обычно рассматривается след оператора. Пусть Aесть С*-алгебра,
обычно рассматривается след оператора. Пусть Aесть С*-алгебра,  -такое представление С*-алгебры А, что Неймана алгебра
-такое представление С*-алгебры А, что Неймана алгебра  порожденная алгеброй
порожденная алгеброй  является фактором полуконечного типа; пусть
является фактором полуконечного типа; пусть  -точный нормальный полуконечный след на
-точный нормальный полуконечный след на  -линейное продолжение следа
-линейное продолжение следа  на идеал
на идеал  если множество
если множество  отлично от нуля, то формула
отлично от нуля, то формула  определяет X. представления алгебры А, ограничение к-рого на А + есть характер С*-алгебры А. Во многих случаях X. представления алгебры определяет представление однозначно с точностью до нек-рого отношения эквивалентности; напр., характер неприводимого конечномерного представления определяет представление однозначно с точностью до эквивалентности; X. фактор представления С*-алгебры, допускающего след, определяет представление однозначно с точностью до квазиэквивалеитности.
определяет X. представления алгебры А, ограничение к-рого на А + есть характер С*-алгебры А. Во многих случаях X. представления алгебры определяет представление однозначно с точностью до нек-рого отношения эквивалентности; напр., характер неприводимого конечномерного представления определяет представление однозначно с точностью до эквивалентности; X. фактор представления С*-алгебры, допускающего след, определяет представление однозначно с точностью до квазиэквивалеитности.