"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХАРАКТЕРЗначение ХАРАКТЕР в математической энциклопедии:
полугруппы - ненулевой гомоморфизм коммутативной полугруппы Sс единицей в мультипликативную полугруппу комплексных чисел, состоящую из всех чисел с модулем 1 и нуля. Иногда под X. полугруппы понимают ненулевой гомоморфизм в мультипликативную полугруппу комплексных чисел, модуль к-рых  Оба понятия X. полугруппы эквивалентны, если S - клиффордова полугруппа. Множество S * всех X. полугруппы Sобразует коммутативную полугруппу с единицей (полугруппу характеров) относительно поточечного умножения * Оба понятия X. полугруппы эквивалентны, если S - клиффордова полугруппа. Множество S * всех X. полугруппы Sобразует коммутативную полугруппу с единицей (полугруппу характеров) относительно поточечного умножения * 
Идеал Рполугруппы Sназ. вполне изолированным, если  есть подполугруппа. Множество всех вполне изолированных идеалов коммутативной полугруппы с единицей образует полурешетку относительно операции объединения, изоморфную полурешетке идемпотентов (см. Идемпотентов полугруппа )полугруппы есть подполугруппа. Множество всех вполне изолированных идеалов коммутативной полугруппы с единицей образует полурешетку относительно операции объединения, изоморфную полурешетке идемпотентов (см. Идемпотентов полугруппа )полугруппы  Характеры коммутативной полугруппы Sотделяют элементы из S, если для любых Характеры коммутативной полугруппы Sотделяют элементы из S, если для любых  найдется найдется  такой, что такой, что  Если Sс единицей, то X. полугруппы Sотделяют элементы из . тогда и только тогда, когда S - сепаративная полугруппа. Задача описания полугруппы X. произвольной коммутативной полугруппы с единицей сводится к описанию X. полугруппы, являющейся полурешеткой групп; соответствующее описание для случая, когда эта полурошетка удовлетворяет условию минимальности, см., напр. [1], з 5.5. Имеется абстрактная характеризация полугрупп X. [2]. Если Sс единицей, то X. полугруппы Sотделяют элементы из . тогда и только тогда, когда S - сепаративная полугруппа. Задача описания полугруппы X. произвольной коммутативной полугруппы с единицей сводится к описанию X. полугруппы, являющейся полурешеткой групп; соответствующее описание для случая, когда эта полурошетка удовлетворяет условию минимальности, см., напр. [1], з 5.5. Имеется абстрактная характеризация полугрупп X. [2].
Для любого  отображение отображение   является X. полугруппы S*, т. е. является X. полугруппы S*, т. е.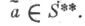 Отображение Отображение  является гомоморфизмом Sв S** (так. наз. канонич. гомоморфизм). Если является гомоморфизмом Sв S** (так. наз. канонич. гомоморфизм). Если  является изоморфизмом S на S**, то говорят, что для . справедлива теорома двойственности. Теорема двойственности справедлива для коммутативной полугруппы Sс единицей тогда и только тогда, когда S- инверсная полугруппа [3]. О вопросах двойственности для X. полугрупп в топологич. случае см. Топологическая полугруппа. является изоморфизмом S на S**, то говорят, что для . справедлива теорома двойственности. Теорема двойственности справедлива для коммутативной полугруппы Sс единицей тогда и только тогда, когда S- инверсная полугруппа [3]. О вопросах двойственности для X. полугрупп в топологич. случае см. Топологическая полугруппа.
Лит.:[1] Клиффорд А., Престон Г., Алгебраическая теория полугрупп, пер. с англ., т. 1, М., 1972; [2] Лесохин М. М., лИзв. вузов. Матем.
|

 Оба понятия X. полугруппы эквивалентны, если S - клиффордова полугруппа. Множество S * всех X. полугруппы Sобразует коммутативную полугруппу с единицей (полугруппу характеров) относительно поточечного умножения *
Оба понятия X. полугруппы эквивалентны, если S - клиффордова полугруппа. Множество S * всех X. полугруппы Sобразует коммутативную полугруппу с единицей (полугруппу характеров) относительно поточечного умножения * 
 есть подполугруппа. Множество всех вполне изолированных идеалов коммутативной полугруппы с единицей образует полурешетку относительно операции объединения, изоморфную полурешетке идемпотентов (см. Идемпотентов полугруппа )полугруппы
есть подполугруппа. Множество всех вполне изолированных идеалов коммутативной полугруппы с единицей образует полурешетку относительно операции объединения, изоморфную полурешетке идемпотентов (см. Идемпотентов полугруппа )полугруппы  Характеры коммутативной полугруппы Sотделяют элементы из S, если для любых
Характеры коммутативной полугруппы Sотделяют элементы из S, если для любых  найдется
найдется  такой, что
такой, что  Если Sс единицей, то X. полугруппы Sотделяют элементы из . тогда и только тогда, когда S - сепаративная полугруппа. Задача описания полугруппы X. произвольной коммутативной полугруппы с единицей сводится к описанию X. полугруппы, являющейся полурешеткой групп; соответствующее описание для случая, когда эта полурошетка удовлетворяет условию минимальности, см., напр. [1], з 5.5. Имеется абстрактная характеризация полугрупп X. [2].
Если Sс единицей, то X. полугруппы Sотделяют элементы из . тогда и только тогда, когда S - сепаративная полугруппа. Задача описания полугруппы X. произвольной коммутативной полугруппы с единицей сводится к описанию X. полугруппы, являющейся полурешеткой групп; соответствующее описание для случая, когда эта полурошетка удовлетворяет условию минимальности, см., напр. [1], з 5.5. Имеется абстрактная характеризация полугрупп X. [2].  отображение
отображение 
 является X. полугруппы S*, т. е.
является X. полугруппы S*, т. е.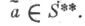 Отображение
Отображение  является гомоморфизмом Sв S** (так. наз. канонич. гомоморфизм). Если
является гомоморфизмом Sв S** (так. наз. канонич. гомоморфизм). Если  является изоморфизмом S на S**, то говорят, что для . справедлива теорома двойственности. Теорема двойственности справедлива для коммутативной полугруппы Sс единицей тогда и только тогда, когда S- инверсная полугруппа [3]. О вопросах двойственности для X. полугрупп в топологич. случае см. Топологическая полугруппа.
является изоморфизмом S на S**, то говорят, что для . справедлива теорома двойственности. Теорема двойственности справедлива для коммутативной полугруппы Sс единицей тогда и только тогда, когда S- инверсная полугруппа [3]. О вопросах двойственности для X. полугрупп в топологич. случае см. Топологическая полугруппа.