"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ХААРА МЕРА
Значение ХААРА МЕРА в математической энциклопедии:
- ненулевая положительная мера 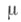 на
на 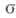 -кольце . подмножеств Елокально компактной группы G, порожденном семейством всех компактных подмножеств, принимающая конечные значения на всех компактных подмножествах в Gи удовлетворяющая либо условию левоинвариантности:
-кольце . подмножеств Елокально компактной группы G, порожденном семейством всех компактных подмножеств, принимающая конечные значения на всех компактных подмножествах в Gи удовлетворяющая либо условию левоинвариантности: 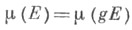 для всех
для всех 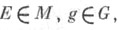 где
где 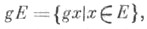 либо условию правоинвариантности:
либо условию правоинвариантности:
 для всех
для всех 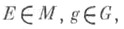 где
где 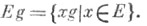
Соответственно говорят о лево- или правоинвариантной X. м. Всякая X. м.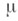 -регулярна, т. е.
-регулярна, т. е.
 для всех
для всех 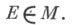
Левоинвариантная (а также правоинвариантная) Х. м. существует и определена однозначно с точностью до положительного множителя; это было установлено А. Хааром [1] (при дополнительном предположении о сепарабельности группы G).
Если f - финитная непрерывная функция на G, то f интегрируема относительно левоинвариантной X. м. на G и соответствующий интеграл левоинвариантен (см. Инвариантное интегрирование), т. е.
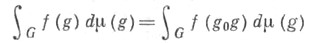 для всех
для всех  Аналогичным свойством обладает правоинвариантная X. м. Мера Хаара всей группы G конечна тогда и только тогда, когда G компактна.
Аналогичным свойством обладает правоинвариантная X. м. Мера Хаара всей группы G конечна тогда и только тогда, когда G компактна.
Если 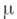 - левоинвариантная X. м. на G, то для любого
- левоинвариантная X. м. на G, то для любого  имеет место равенство
имеет место равенство
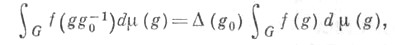 где
где  - непрерывный гомоморфизм группы G в мультипликативную группу R+ положительных действительных чисел, не зависящий от выбора непрерывной финитной функции f на G. Гомоморфизм
- непрерывный гомоморфизм группы G в мультипликативную группу R+ положительных действительных чисел, не зависящий от выбора непрерывной финитной функции f на G. Гомоморфизм  наз. модулем группы G; мера
наз. модулем группы G; мера 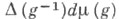 является правоинвариантной X. м. на G. Если
является правоинвариантной X. м. на G. Если  то группа Gназ. унимодулярной; в этом случае левоинвариантная X. м. является также и правоинвариантной и наз. двусторонне инвариантной. В частности, любая компактная, дискретная и абелева локально компактная группа, а также любая связная полупростая или нильпотентная группа Ли унимодулярна. Унимодулярность группы G равносильна также тому, что любая левоинвариантная Х. м.
то группа Gназ. унимодулярной; в этом случае левоинвариантная X. м. является также и правоинвариантной и наз. двусторонне инвариантной. В частности, любая компактная, дискретная и абелева локально компактная группа, а также любая связная полупростая или нильпотентная группа Ли унимодулярна. Унимодулярность группы G равносильна также тому, что любая левоинвариантная Х. м. 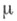 на G инверсионно инвариантна, т. е.
на G инверсионно инвариантна, т. е. 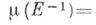
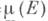 для всех
для всех 
Если G - группа Ли, то интеграл но левоинвариантной (правоинвариантной) X. м. на G определяется формулой
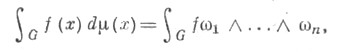 где
где 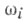 - линейно независимые левоинвариантные (правоинвариантные) дифференциальные формы 1-го порядка на G (см. Маурера - Картана форма), п=dimG. Модуль группы Ли G определяется формулой
- линейно независимые левоинвариантные (правоинвариантные) дифференциальные формы 1-го порядка на G (см. Маурера - Картана форма), п=dimG. Модуль группы Ли G определяется формулой
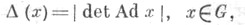 где Ad - присоединенное представление.
где Ad - присоединенное представление.
Примеры. 1) X. м. на аддитивной группе  и на факторгруппе
и на факторгруппе  (группа вращений окружности) совпадает с обычной лебсговской мерой. 2) Полная линейная группа
(группа вращений окружности) совпадает с обычной лебсговской мерой. 2) Полная линейная группа 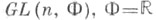 или С, унимодулярна, причем X. м. имеет вид
или С, унимодулярна, причем X. м. имеет вид
 где k=n при
где k=n при  и k=2n при
и k=2n при  a dx - лебеговская мора в евклидовом пространстве всех матриц порядка . над полем Ф.
a dx - лебеговская мора в евклидовом пространстве всех матриц порядка . над полем Ф.
Если G - локально компактная группа, H - ее замкнутая подгруппа, X - однородное пространство G/H, 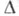 и
и  - модули групп Gи Н соответственно,
- модули групп Gи Н соответственно, 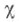 - непрерывным гомоморфизм группы G в
- непрерывным гомоморфизм группы G в  задаваемый формулой
задаваемый формулой
 то существует положительная мера v на
то существует положительная мера v на 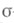 -кольце . множеств
-кольце . множеств  порожденном семейством компактных подмножеств в X, однозначно определяемая условием:
порожденном семейством компактных подмножеств в X, однозначно определяемая условием:
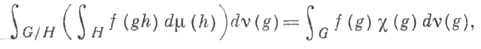
где f - любая непрерывная финитная функция на G,  причем
причем
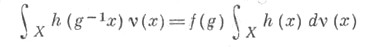
для всех непрерывных финитных функций f на X.
Лит.: [1] Нааr A., лAnn. Math.

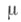 на
на 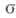 -кольце . подмножеств Елокально компактной группы G, порожденном семейством всех компактных подмножеств, принимающая конечные значения на всех компактных подмножествах в Gи удовлетворяющая либо условию левоинвариантности:
-кольце . подмножеств Елокально компактной группы G, порожденном семейством всех компактных подмножеств, принимающая конечные значения на всех компактных подмножествах в Gи удовлетворяющая либо условию левоинвариантности: 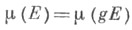 для всех
для всех 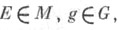 где
где 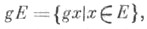 либо условию правоинвариантности:
либо условию правоинвариантности:  для всех
для всех 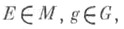 где
где 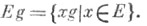
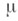 -регулярна, т. е.
-регулярна, т. е.  для всех
для всех 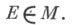
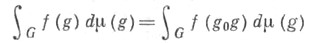 для всех
для всех  Аналогичным свойством обладает правоинвариантная X. м. Мера Хаара всей группы G конечна тогда и только тогда, когда G компактна.
Аналогичным свойством обладает правоинвариантная X. м. Мера Хаара всей группы G конечна тогда и только тогда, когда G компактна. 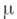 - левоинвариантная X. м. на G, то для любого
- левоинвариантная X. м. на G, то для любого  имеет место равенство
имеет место равенство 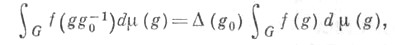 где
где  - непрерывный гомоморфизм группы G в мультипликативную группу R+ положительных действительных чисел, не зависящий от выбора непрерывной финитной функции f на G. Гомоморфизм
- непрерывный гомоморфизм группы G в мультипликативную группу R+ положительных действительных чисел, не зависящий от выбора непрерывной финитной функции f на G. Гомоморфизм  наз. модулем группы G; мера
наз. модулем группы G; мера 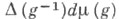 является правоинвариантной X. м. на G. Если
является правоинвариантной X. м. на G. Если  то группа Gназ. унимодулярной; в этом случае левоинвариантная X. м. является также и правоинвариантной и наз. двусторонне инвариантной. В частности, любая компактная, дискретная и абелева локально компактная группа, а также любая связная полупростая или нильпотентная группа Ли унимодулярна. Унимодулярность группы G равносильна также тому, что любая левоинвариантная Х. м.
то группа Gназ. унимодулярной; в этом случае левоинвариантная X. м. является также и правоинвариантной и наз. двусторонне инвариантной. В частности, любая компактная, дискретная и абелева локально компактная группа, а также любая связная полупростая или нильпотентная группа Ли унимодулярна. Унимодулярность группы G равносильна также тому, что любая левоинвариантная Х. м. 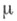 на G инверсионно инвариантна, т. е.
на G инверсионно инвариантна, т. е. 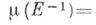
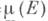 для всех
для всех 
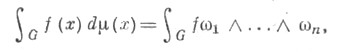 где
где 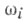 - линейно независимые левоинвариантные (правоинвариантные) дифференциальные формы 1-го порядка на G (см. Маурера - Картана форма), п=dimG. Модуль группы Ли G определяется формулой
- линейно независимые левоинвариантные (правоинвариантные) дифференциальные формы 1-го порядка на G (см. Маурера - Картана форма), п=dimG. Модуль группы Ли G определяется формулой 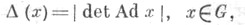 где Ad - присоединенное представление.
где Ad - присоединенное представление.  и на факторгруппе
и на факторгруппе  (группа вращений окружности) совпадает с обычной лебсговской мерой. 2) Полная линейная группа
(группа вращений окружности) совпадает с обычной лебсговской мерой. 2) Полная линейная группа 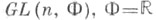 или С, унимодулярна, причем X. м. имеет вид
или С, унимодулярна, причем X. м. имеет вид  где k=n при
где k=n при  и k=2n при
и k=2n при  a dx - лебеговская мора в евклидовом пространстве всех матриц порядка . над полем Ф.
a dx - лебеговская мора в евклидовом пространстве всех матриц порядка . над полем Ф. 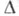 и
и  - модули групп Gи Н соответственно,
- модули групп Gи Н соответственно, 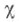 - непрерывным гомоморфизм группы G в
- непрерывным гомоморфизм группы G в  задаваемый формулой
задаваемый формулой  то существует положительная мера v на
то существует положительная мера v на 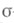 -кольце . множеств
-кольце . множеств  порожденном семейством компактных подмножеств в X, однозначно определяемая условием:
порожденном семейством компактных подмножеств в X, однозначно определяемая условием: 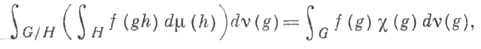
 причем
причем