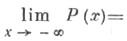"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУРЬЕ - СТИЛТЬЕСА ПРЕОБРАЗОВАНИЕ
Значение ФУРЬЕ - СТИЛТЬЕСА ПРЕОБРАЗОВАНИЕ в математической энциклопедии:
- одно из интегральных преобразований, родственное Фурье преобразованию. Пусть функция F(х)имеет ограниченное изменение на  Функция
Функция

наз. преобразованием Фурье - Стилтьеса для F. Функция 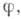 определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция
определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция 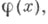 разлагающаяся в ряд Фурье
разлагающаяся в ряд Фурье  с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с
с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с 
Формула (*) допускает обращение: если F(х)имеет ограниченное изменение и

то
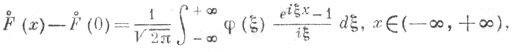
где интеграл понимается в смысле главного значения на 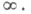
Если в формуле (*) в качестве функции F(х)допустить лишь неубывающие функции ограниченной вариации, то совокупность получающихся непрерывных функций 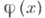 полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство
полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство
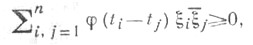
каковы бы ни были комплексные числа  (теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию
(теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию

подчиняют дополнительным ограничениям
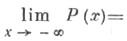

непрерывна слева, и именуют распределением, функцию

- характеристической функцией [распределения Р(х)].Теорема Бохнера-Хинчина выражает тогда необходимое и достаточное условие того, что непрерывная функция Ф(х)[для к-рой Ф(0)=1] является характеристической функцией нек-рого распределения.
Теория Ф.-С. п. развита и в n-мерном случае.
Лит.:[1] Бохнер С., Лекции об интегралах Фурье, пер. с англ., М., 1962; [2] Зигмунд А., Тригонометрические ряды, пер. с англ.. т. 2, М., 1965; [3] Гнеденко Б. В., Курс теории вероятностей, 5 изд., М., 1969.
П. И. Лизоркин.

 Функция
Функция 
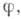 определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция
определенная интегралом (1), ограниченна и непрерывна. Всякая периодич. функция 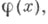 разлагающаяся в ряд Фурье
разлагающаяся в ряд Фурье  с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с
с абсолютно сходящимся рядом коэффициентов, может быть записана в форме интеграла (*) с 

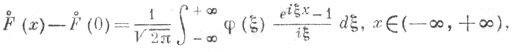
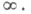
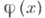 полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство
полностью характеризуется свойством: для любой системы действительных чисел t1,. . .,tn справедливо неравенство 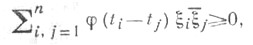
 (теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию
(теорема Бохнера - Xинчина). Такие функции наз. положительно определенными. Ф.-С. п. находит широкое применение в теории вероятностей, где неубывающую функцию