"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ФУРЬЕ - БЕССЕЛЯ ИНТЕГРАЛЗначение ФУРЬЕ - БЕССЕЛЯ ИНТЕГРАЛ в математической энциклопедии:
интеграл Ганкеля,- аналог Фурье интеграла для Бесселя функций, имеющий вид 
Формула (*) может быть получена из Фурье-Бесселя ряда для интервала (0, l)переходом к пределу при   Г. Ганкель (Н. Hankel, 1875) установил теорему: если функция f(x)кусочно непрерывная и имеет ограниченную вариацию на любом интервале 0<х<l, интеграл Г. Ганкель (Н. Hankel, 1875) установил теорему: если функция f(x)кусочно непрерывная и имеет ограниченную вариацию на любом интервале 0<х<l, интеграл 
сходится, то формула (*) справедлива при v >-1/2 во всех точках непрерывности f(х),  В точках разрыва х 0, В точках разрыва х 0,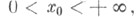 правая часть формулы (*) равна [f(x0 - 0)+f(x0 + 0)]/2, при x0 = 0 она дает f(0+)/2. Аналоги Ф. - Б. и. (*) для цилиндрич. функций Zv (х)других типов также справедливы, но пределы интегралов должны быть соответственно изменены. правая часть формулы (*) равна [f(x0 - 0)+f(x0 + 0)]/2, при x0 = 0 она дает f(0+)/2. Аналоги Ф. - Б. и. (*) для цилиндрич. функций Zv (х)других типов также справедливы, но пределы интегралов должны быть соответственно изменены.
Е. Д. Соломенцее.
|



 Г. Ганкель (Н. Hankel, 1875) установил теорему: если функция f(x)кусочно непрерывная и имеет ограниченную вариацию на любом интервале 0<х<l, интеграл
Г. Ганкель (Н. Hankel, 1875) установил теорему: если функция f(x)кусочно непрерывная и имеет ограниченную вариацию на любом интервале 0<х<l, интеграл 
 В точках разрыва х 0,
В точках разрыва х 0,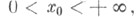 правая часть формулы (*) равна [f(x0 - 0)+f(x0 + 0)]/2, при x0 = 0 она дает f(0+)/2. Аналоги Ф. - Б. и. (*) для цилиндрич. функций Zv (х)других типов также справедливы, но пределы интегралов должны быть соответственно изменены.
правая часть формулы (*) равна [f(x0 - 0)+f(x0 + 0)]/2, при x0 = 0 она дает f(0+)/2. Аналоги Ф. - Б. и. (*) для цилиндрич. функций Zv (х)других типов также справедливы, но пределы интегралов должны быть соответственно изменены.